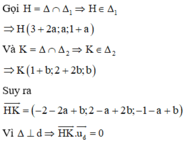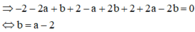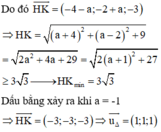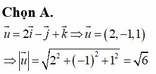Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Phương pháp:
Vecto u → = x . i → + y . j → + z . k → có tọa độ u → = x ; y ; z
Cho hai vecto a → = x 1 ; y 1 ; z 1 , b → = x 2 ; y 2 ; z 2 ⇒ a → . b → = x 1 x 2 + y 1 y 2 + z 1 z 2
Cách giải:
b → = i → − 3 k → ⇒ b → = 1 ; 0 ; − 3
Khi đó,
a → . b → = 2.1 + − 1 .0 + 4. − 3 = − 10

Giả sử
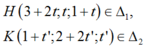
ta có:
![]()
Đường thẳng d có 1 VTCP là u d → 1 ; 1 ; - 2
Vì

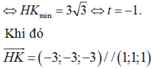
Suy ra đường thẳng ∆ nhận u → 1 ; 1 ; 1 là 1 VTCP h = k = 1
Vậy h - k = 1 - 1 = 0
Chọn A.

Rõ ràng a → và b → không cùng phương.
Ba vectơ a → , b → , c → đồng phẳng ⇔ ∃ cặp số ( m,n ) sao cho c → = m a → + n b →
Vì u → , v → , w → không đồng phẳng nên
x - m + n = 0 1 - 2 m - n = 0 - 2 - 3 m - n = 0 ⇔ x = - 10
Đáp án B