Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta có:
Để hàm \(y=m\sin x-n\cos x-3x\) nghịch biến trên R thì:
\(y'=m\cos x+n\sin x-3\leq 0, \forall x\in\mathbb{R}\)
\(\Leftrightarrow m\cos x+n\sin x\leq 3\), \(\forall x\in\mathbb{R}\)
\(\Rightarrow (m\cos x+n\sin x)_{\max}\le 3(*)\)
Ta thấy theo BĐT Bunhiacopxky:
\((m\cos x+n\sin x)^2\leq (m^2+n^2)(\cos ^2x+\sin ^2x)\)
hay \((m\cos x+n\sin x)^2\leq m^2+n^2\)
\(\Rightarrow m\cos x+n\sin x\leq \sqrt{m^2+n^2}\).
Do đó \((m\cos x+n\sin x)_{\max}=\sqrt{m^2+n^2}(**)\)
Từ (*) và (**) suy ra để \(y'\leq 0\) thì \(\sqrt{m^2+n^2}\leq 3\Leftrightarrow m^2+n^2\leq 9\)
Đáp án C.

Chọn C
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
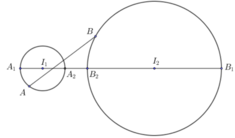
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8

- Với \(a=b=0\) thỏa mãn
- Với \(a=0;b\ne0\) hàm bậc 3 ko tồn tại min max (ko thỏa mãn)
- Với \(a< 0\Rightarrow\lim\limits_{x\rightarrow\infty}f\left(x\right)=-\infty\Rightarrow\) ko tồn tại min f(x) (loại)
\(\Rightarrow a>0\)
\(f\left(0\right)=-3\Rightarrow\) để hàm thỏa mãn yêu cầu thì \(f\left(x\right)\ge-3;\forall x\ne0\)
\(\Leftrightarrow ax^4+bx^3+x^2\ge0\Leftrightarrow x^2\left(ax^2+bx+1\right)\ge0\)
\(\Leftrightarrow ax^2+bx+1\ge0\)
\(\Leftrightarrow\Delta=b^2-4a\le0\Leftrightarrow b^2\le4a\)
- Với \(a=1\Rightarrow-2\le b\le2\) có 5 cặp
- Với \(a=2\Rightarrow-2\le b\le2\) có 5 cặp
- Với \(a=3\Rightarrow-3\le b\le3\) có 7 cặp
- Với \(a=4\Rightarrow-4\le b\le4\) có 9 cặp
Vậy tổng cộng có 27 cặp a;b thỏa mãn

Lời giải:
Để hai hàm số cắt nhau tại hai điểm phân biệt thì phương trình
\(\frac{x+1}{x-1}+(2x-m)=0\Leftrightarrow 2x^2-(m+1)x+(m+1)=0\) có hai nghiệm phân biệt
\(\Rightarrow \Delta =(m+1)^2-8(m+1)>0\Leftrightarrow m>7\) hoặc $m<-1$
Hai điểm $A,B$ có hoành độ tương ứng với nghiệm của phương trình giao điểm. Do đó áp dụng hệ thức Viet: \(x_A+x_B=\frac{m+1}{2}\)
Hoành độ trung điểm $AB$ là \(\frac{x_A+x_B}{2}=\frac{m+1}{4}=\frac{5}{2}\Rightarrow m=9\)
Do đó đáp án $C$ là đáp án đúng

\(z=x+i.y\) với \(x=3y\)
\(\Rightarrow x-3y=0\Rightarrow\) tập hợp z là một đường thẳng






Đáp án B