Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có:
\(\widehat{A}+\widehat{C}=180^o\) ( góc đối của tứ giác nội tiếp )
\(\Rightarrow\widehat{C}=180^o-80^o=100^o\)
Ta có:
\(\widehat{B}+\widehat{D}=180^o\) ( góc đối của tứ giác nội tiếp )
\(\Rightarrow\widehat{D}=180^o-60^o=120^o\)
Vì tứ giác ABCD nội tiếp (O)
=> góc B + góc C = 180 độ (tổng 2 góc đối bằng 180 độ)
=> 60 + góc C = 180
=> góc C = 180 - 60 = 120 độ
Tiếp tục, ta cũng có góc A + góc D = 180 độ
=> 75 + góc D = 180
=> góc D = 180 - 75 = 105 độ
Note: Bài này đoạn kết còn có cách tính khác, cần inbox mình
Theo mk thi: goc C=105° va goc D=120°
Aj thay dung thj ung ho mk nha!!! Cam on.
Do tứ giác ABCD nội tiếp \(\Rightarrow B+D=180^0\) (1)
Mà \(\dfrac{B}{D}=\dfrac{2}{3}\Rightarrow B=\dfrac{2}{3}D\)
Thế vào (1):
\(\dfrac{2}{3}D+D=180^0\Rightarrow\dfrac{5}{3}D=180^0\)
\(\Rightarrow D=108^0\)
\(B=\dfrac{2}{3}D=\dfrac{2}{3}.108^0=72^0\)
b) Xét ΔFDC có
A\(\in\)FD(gt)
B\(\in\)FC(gt)
AB//CD(gt)
Do đó: \(\dfrac{FA}{AD}=\dfrac{FB}{BC}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{FA}{FB}=\dfrac{AD}{BC}=1\)
hay FA=FB
Ta có: FA+AD=FD(A nằm giữa F và D)
FB+BC=FC(B nằm giữa F và C)
mà FA=FB(cmt)
và AD=BC(ABCD là hình thang cân)
nên FD=FC
Ta có: FA=FB(cmt)
FD=FC(cmt)
Do đó: \(FA\cdot FD=FB\cdot FC\)(đpcm)
a) Ta có: ABCD là tứ giác nội tiếp(gt)
nên \(\widehat{A}+\widehat{C}=180^0\)(hai góc đối)(1)
Ta có: ABCD là hình thang(AB//CD)
nên \(\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)(2)
Từ (1) và (2) suy ra \(\widehat{C}=\widehat{D}\)
Hình thang ABCD(AB//CD) có \(\widehat{C}=\widehat{D}\)(cmt)
nên ABCD là hình thang cân(Dấu hiệu nhận biết hình thang cân)
cho tứ giác ABCD nội tiếp đường tròn (O) . Biết góc A= 80 độ , B= 125 độ
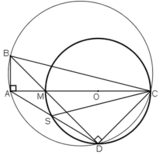
a)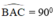 
⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC
⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
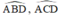đều là góc nội tiếp chắn cung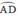 
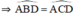
c) + Trong đường tròn đường kính MC:
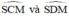đều là các góc nội tiếp cùng chắn cung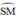 
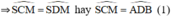
+ Trong đường tròn đường kính BC:
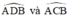đều là các góc nội tiếp chắn cung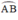 
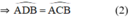
có \(\widehat{AEH}=90\)
\(\widehat{AFH}\)=90
\(\widehat{AEH}+\widehat{AFH}=90+90=180\) tổng 2 góc đối nhau
⇒ tứ giác AEHF là tứ giác nội tiếp
a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Ta có:
\(\widehat{A}+\widehat{C}=180^o\) ( góc đối của tứ giác nội tiếp )
\(\Leftrightarrow55^o+\widehat{C}=180^o\)
\(\Rightarrow\widehat{C}=180^o-55^o=125^o\)
Ta có:
\(\widehat{B}+\widehat{D}=180^o\) ( góc đối của tứ giác nội tiếp )
\(\Leftrightarrow\widehat{B}+65^o=180^o\)
\(\Rightarrow\widehat{B}=180^o-65^o=115^o\)