Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
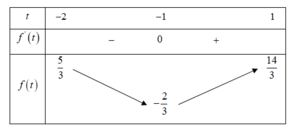
Xét f(x) = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] ta có:
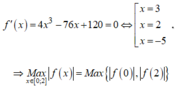
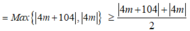
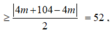
Dấu “=” xảy ra khi và chỉ khi ![]()
Nhận xét: Với trắc nghiệm thì ta thử đáp án được đáp án B

Chọn A
Vì tam giác SAC vuông tại A
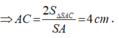
![]()
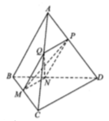
nên tam giác ABC vuông tại A. Chọn hệ trục Oxyz như hình vẽ
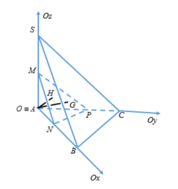
Ta có
A(0;0;0), B(3;0;0), C(0;4;0), S(0;0;3)
Vì G là trọng tâm của tứ diện SABC nên ta có
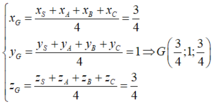
Gọi H là hình chiếu của điểm A lên mặt phẳng α . Theo tính chất của tam diện vuông ta có
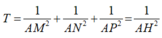
![]()
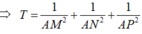
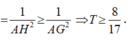
Dấu “=” xảy ra khi H ≡ G tức mặt phẳng α đi qua điểm G và vuông góc với đường thẳng OG.
Vậy giá trị nhỏ nhất của T bằng 8 17
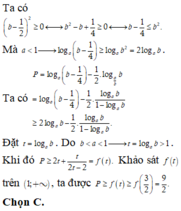
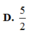

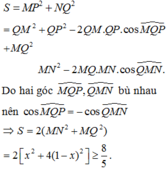
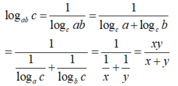
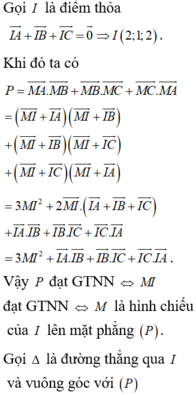
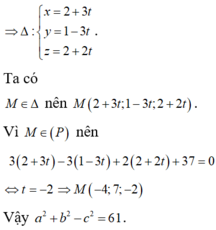
Lời giải:
Đặt \(\left\{\begin{matrix} \log_ab=x\\ \log_bc=y\\ \log_ca=z\end{matrix}\right.\Rightarrow \left\{\begin{matrix} \log_ba=\frac{1}{x}\\ \log_cb=\frac{1}{y}\\ \log_ac=\frac{1}{z}\end{matrix}\right. \). và \(xyz=1\)
Do \(a,b,c>1\Rightarrow x,y,z>0\)
Ta có:
\(P=\log_a(bc)+\log_b(ac)+4\log_c(ab)\)
\(=\log_ab+\log_ac+\log_ba+\log_bc+4\log_ca+4\log_cb\)
\(=x+\frac{1}{z}+\frac{1}{x}+y+4z+\frac{4}{y}\)
Áp dụng BĐT Cô-si cho các số dương:
\(\left\{\begin{matrix} x+\frac{1}{x}\geq 2\sqrt{1}=2\\ y+\frac{4}{y}\geq 2\sqrt{4}=4\\ \frac{1}{z}+4z\geq 2\sqrt{4}=4\end{matrix}\right.\) \(\Rightarrow P\geq 2+4+4=10\)
\(\Rightarrow m=10\)
Dấu bằng xảy ra khi \(\left\{\begin{matrix} x=\frac{1}{x}\rightarrow x=1\\ y=\frac{4}{y}\rightarrow y=2\\ \frac{1}{z}=4z\rightarrow z=\frac{1}{2}\end{matrix}\right.\) (thỏa mãn)
Suy ra \(n=\log_bc=y=2\)
\(\Rightarrow m+n=12\)