Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

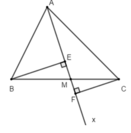
Vì BE ⊥ Ax tại E nên tam giác BEM vuông tại E ⇒ BM > BE (quan hệ đường xiên và đường vuông góc)
Vì CF ⊥ Ax tại F nên tam giác CFM vuông tại F ⇒ CM > CF (quan hệ đường xiên và đường vuông góc)
Khi đó ta có: BM + CM > BE + CF
Mà BM + CM = BC (M thuộc BC)
Do đó: BC > BE + CF hay BE + CF < BC.
Chọn đáp án A

Bạn kiểm tra lại đề nhé! Tia Ax nằm giữa hai tia AD và AC hay hai tia AB và AC
Tham khảo đề bài và lời giải tại link:
Câu hỏi của Chử Văn Dũng - Toán lớp 7 - Học toán với OnlineMath

a)xét tgAEB và tgADC có
A là góc chung
AE=AC(gt)
AB=AD(gt)
suy ra tgAEB = tgADC (c.g.c)
suy ra BE=AC(hai cạnh tương ứng
cho k trước đi rồi làm câu b;c;d cho

`a,`
Ta có: \(\left\{{}\begin{matrix}\text{BE }\bot\text{ Ax}\\\text{CF }\bot\text{ Ax}\end{matrix}\right.\)
`@` Theo tiên đề Euclid
`-> \text {BE // CF}`
`b,`
Xét `2 \Delta` vuông `BEM` và `CFM`:
`\text {MB = MC (M là trung điểm của BC)}`
$\widehat {BME} = \widehat {CMF} (\text {2 góc đối đỉnh})$
`=> \Delta BEM = \Delta CFM (ch-gn)`
`c,`
Vì `\Delta BEM = \Delta CFM (b)`
`-> \text {BE = CF (2 cạnh tương ứng)}`
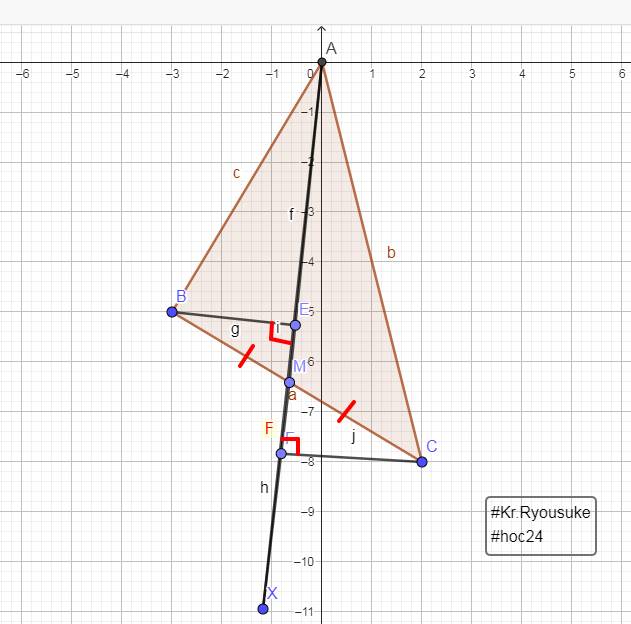
a:BE vuông góc AM
CF vuông góc AM
=>BE//CF
b: Xet ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
góc BME=góc CMF
=>ΔBEM=ΔCFM
b: ΔBEM=ΔCFM
=>BE=CF
Tớ nghĩ đề đúng phải là \(BE+CF\le BC\)
Bạn xem lại đề nhé