K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

27 tháng 10 2021
Sửa đề \(\sqrt{a^2+bc}+\sqrt{b^2+ca}+\sqrt{c^2+ab}\le6\)
\(\sqrt{a^2+3b}=\sqrt{a^2+\left(a+b+c\right)b}=\sqrt{a^2+ab+b^2+bc}\\ =\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{a+b+a+c}{2}=\dfrac{2a+b+c}{2}\)
Cmtt \(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{b^2+3c}\le\dfrac{a+2b+c}{2}\\\sqrt{c^2+3a}\le\dfrac{a+b+2c}{2}\end{matrix}\right.\)
Cộng VTV:
\(\Leftrightarrow VT\le\dfrac{2a+b+c+a+2b+c+a+b+2c}{2}\\ \Leftrightarrow VT\le\dfrac{4\left(a+b+c\right)}{2}=2\left(a+b+c\right)=6\)
Dấu \("="\Leftrightarrow a=b=c=1\)
LY
27 tháng 10 2021
em chưa hiểu cách biến đổi của cái này ạ\(\sqrt{a^2+ab+b^2+bc}=\sqrt{\left(a+b\right)\left(a+c\right)}\)

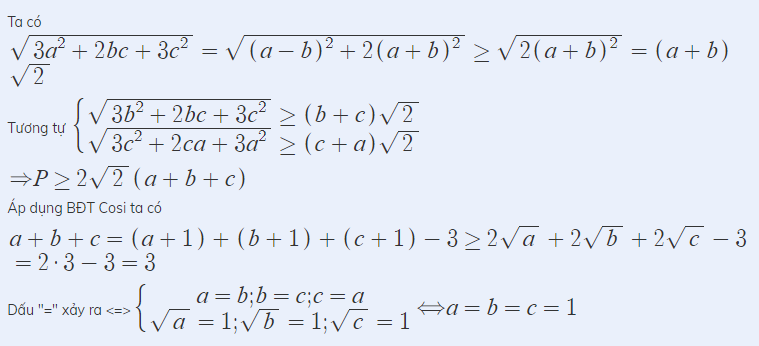
Dự đoán điểm rơi \(a=b=c=4\) .
Áp dụng BĐT AM-GM ta có :
\(\left\{{}\begin{matrix}a+4\ge4\sqrt{a}\\b+4\ge4\sqrt{b}\\c+4\ge4\sqrt{c}\end{matrix}\right.\Rightarrow2\sqrt{a}+2\sqrt{b}+2\sqrt{c}\le\dfrac{a+b+c+12}{2}\)
Áp dụng BĐT Bu-nhi-a-cốp-xki ta có :
\(\sqrt{3a+2\sqrt{a}+1}+\sqrt{3b+2\sqrt{b}+1}+\sqrt{3c+2\sqrt{c}+1}\le\sqrt{3.\left[3\left(a+b+c\right)+2\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)+3\right]}=\sqrt{3.\left(3.12+12+3\right)}=3\sqrt{17}\)
Vậy BĐT đã được chứng minh !
Hơi khoai :))))))
DƯƠNG PHAN KHÁNH DƯƠNG cảm ơn nha ^-^