Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔACN có
AB=AC
góc A chung
AM=AN
=>ΔABM=ΔACN
b: Xét ΔABC có
BM,CN là trung tuyến
BM cắt CN tại I
=>I là trọng tam
=>H là trung điểm của BC
ΔABC cân tại A
mà AH là trung tuyến
nên AH vuông góc BC

a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{BAM}\) chung
AM=AN
Do đó: ΔABM=ΔACN
Suy ra: BM=CN
b: Xét ΔNBC và ΔMCB có
NB=MC
BC chung
NC=MB
Do đó: ΔNBC=ΔMCB
Suy ra: \(\widehat{ICB}=\widehat{IBC}\)
=>ΔIBC cân tại I
=>IB=IC
mà AB=AC
nên AI là đường trung trực của BC
=>H là trung điểm của BC

Tham khảo:
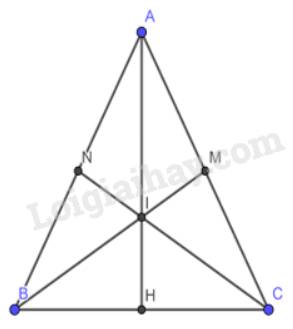
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.
Vì AB = AC (tính chất tam giác cân)
\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)
Xét tam giác AMB và tam giác ANC ta có :
AM = AN (cmt)
AB = AC
Góc A chung
\( \Rightarrow \Delta AMB =\Delta ANC\)
\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của BM và CN
\( \Rightarrow \) I là trọng tâm của tam giác ABC
\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC
\( \Rightarrow \) H là trung điểm của BC

a) Xét ΔABK vuông tại B và ΔACK vuông tại C có
AK chung
AB=AC(ΔABC đều)
Do đó: ΔABK=ΔACK(cạnh huyền-cạnh góc vuông)

b: Xét tứ giác ABCE có
M là trung điểm chung của AC và BE
=>ABCE là hình bình hành
=>CE//AB
c: Xét ΔHAB vuông tại H và ΔHKC vuông tại H có
HB=HC
góc HAB=góc HKC
=>ΔHAB=ΔHKC
=>HA=HK
Xét tứ giác ABKC có
H là trung điểm chung của BC và AK
AB=AC
=>ABKC là hình thoi
=>AC=CK
Xét ΔABC có
BM,AH là trung tuyến
BM cắt AH tại G
=>G là trọng tâm
=>3GH=AH
3GH+HC=AH+HC>AC=CK

a. vì tam giác ABC cân tại A
=> AB = AC
=> góc ABC = góc ACB
BM và CN là 2 đường trung tuyến của tam giác ABC
=> N và M lần lượt là trung điểm của AB và AC
=> AN = BN
AM = CM
mà AB = AC
=> AN = BN = AM = CM
Xét tam giác BNC và tam giác CMB:
BC chung
góc ABC = góc ACB (cmt)
BN = CM (cmt)
=> tam giác BNC = tam giác CMB (c-g-c) (đpcm)
b. tam giác BNC = tam giác CMB (cmt)
=> BM = CN ( 2 cạnh tương ứng)
mà BM giao CN tại K
=> K là trọng tâm của tam giác ABC
=> BK = CK
Xét Δ AKB và Δ AKC:
AK chung
AB = AC (cmt)
BK = CK (cmt)
=> Δ AKB = Δ AKC (c-c-c)
=> góc BAK = góc CAK (2 góc tương ứng)
=> AK là tia phân giác góc BAC
=> AK là đường trung trực của Δ ABC
=> AK ⊥ BC (đpcm)
c. Vì AK (AH) ⊥ BC
=> tam giác ABH vuông tại H
mà AH là đường trung trực của tam giác ABC
=> BH = CH = \(\dfrac{BC}{2}=\dfrac{6}{2}=3cm\)
Áp dùng định lí Py - ta - go vào tam giác ABH:
AB2 = BH2 + AH2
52 = 32 + AH2
AH2 = 52 - 32 = 25 - 9 = 16
=> AK = 4cm (AH > 0)
giúp vs chứ mai thi r !!!