Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

từ đề suy ra:
\(\widehat{BAC}=\widehat{DAC}.2=30^o.2=60^o\)
\(\widehat{ABC}=2.\widehat{EBC}=2.30^o=60^o\)
áp dụng đl tổng 3 góc trong của một tam giác :
\(\widehat{ACB}+\widehat{BAC}+\widehat{ABC}=180^o\)
\(\widehat{ACB}+60^o+60^o=180^o\)
\(\Rightarrow\widehat{ACB}=60^o\)
Xét tam giác ABC có 3 góc trong đều bằng nhau và bằng 60\(^o\)
suy ra : ABC là tam giác đều(đpcm)

Tự vẽ hình
Xét hai tam giác ADB\((\widehat{ADB}=90^O)\) và AEC\((\widehat{AEC=90^O)}\) có:
AB = AC (do tam giác ABC cân tại A)
\(\widehat{A}\):góc chung
=>Tam giác ADB=tam giác AEC (...)
=>AD=AE ( hai cạnh tương ứng )

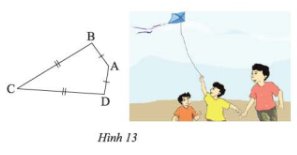
a) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)

Kẻ AF và CG cùng vuông góc với BD, CH vuông góc với AE.
Xét tam giác ABF và tam giác CAH có:
AFB=CHA=90
AB=CA (vì tam giác abc cân tại A)
ABF=CAH (gt)
=>Tam giác ABF=Tam giác CAH (ch-gn)
=>AF=CH (2 cạnh tương ứng) (1)
Xét tam giác ADF và tam giác CDG có:
AFD=CGD=90
AD=CD (vì D là trung điểm của AC)
ADF=CDG (2 góc đối đỉnh)
=>Tam giác ADF=Tam giác CDG (ch-gn)
=>AF=CG (Hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: CH=CG
Xét tam giác CEH và tam giác CEG có:
CH=CG (cmt)
CHE=CGE=90
EC cạnh chung
=>Tam giác CEH=Tam giác CEG (ch-cgv)
=>CEH=CEG (hai góc tương ứng)
Mà CEH là góc ngoài đỉnh E của tam giác AEC
CEG là góc ngoài đỉnh E của tam giác BEC
=>CEH=ECA+EAC và CEG=EBC+ECB
=>ECA+EAC=EBC+ECB (vì CEH+CEG cmt)
=>ECA+EBA=EBC+ECB (vì DAE=ABD) (1)
Lại có: Tam giác ABC cân tại A =>ACB=ABC
=>ECA+ECB=EBC+EBA (2)
Cộng vế theo vế đẳng thức (1) và (2), ta được:
ECA+EBA+ECA+ECB=EBC+ECB+EBC+EBA
=>2ECA+EBA+ECB=2EBC+ECB+EBA
=>2ECA=2EBC
=>ECA=EBC (ĐPCM)