Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

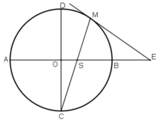
+ M S E ^ là góc có đỉnh S ở trong đường tròn (O)
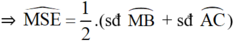
+ E S M ^ là góc tạo bởi tiếp tuyến ME và đây MC
⇒ E M S ^ = 1 2 . s đ M C ⏜ = 1 2 . s đ M B ⏜ + s đ B C ⏜


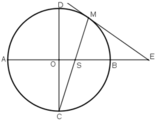

Kiến thức áp dụng
+ Số đo của góc có đỉnh bên trong đường tròn bằng một nửa tổng số đo của hai cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng một nửa số đo của cung bị chắn.

Ta có \(\widehat{MSE}\) = ![]() (1)
(1)
( vì \(\widehat{MSE}\) là góc có đỉnh S ở trong đường tròn (O))
\(\widehat{CME}\) = ![]() =
= ![]() (2)
(2)
(\(\widehat{CME}\) là góc tạo bởi tiếp tuyến và dây cung).
Theo giả thiết ![]() =
= ![]() (3)
(3)
Từ (1), (2), (3) ta có: \(\widehat{MSE}\)= \(\widehat{CME}\)từ đó \(\Delta\)ESM là tam giác cân và ES = EM

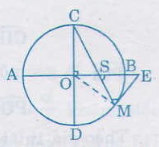
Ta có =
![]() (1)
(1)
( vì là góc có đỉnh S ở trong đường tròn (O))
=
![]() =
= ![]() (2)
(2)
( là góc tạo bởi tiếp tuyến và dây cung).
Theo giả thiết ![]() =
= ![]() (3)
(3)
Từ (1), (2), (3) ta có: =
từ đó ∆ESM là tam giác cân và ES = EM

a: Ta có: ΔOAC vuông tại O
=>\(OA^2+OC^2=AC^2\)
=>\(AC^2=R^2+R^2=2R^2\)
=>\(AC=R\sqrt{2}\)
b: Xét (O) có
\(\widehat{BKM}\) là góc có đỉnh ở trong đường tròn chắn hai cung BM và CA
=>\(\widehat{BKM}=\dfrac{1}{2}\left(sđ\stackrel\frown{BM}+sđ\stackrel\frown{CA}\right)\)
=>\(\widehat{IKM}=\dfrac{1}{2}\cdot\left(sđ\stackrel\frown{BM}+sđ\stackrel\frown{BC}\right)=\dfrac{1}{2}\cdot sđ\stackrel\frown{MC}\left(1\right)\)
Xét (O) có
\(\widehat{IMC}\) là góc tạo bởi tiếp tuyến MI và dây cung MC
Do đó: \(\widehat{IMK}=\dfrac{1}{2}\cdot sđ\stackrel\frown{MC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{IKM}=\widehat{IMK}\)
=>IM=IK
c: \(\widehat{IKM}=\dfrac{1}{2}\left(sđ\stackrel\frown{BM}+sđ\stackrel\frown{AC}\right)\)
\(=\dfrac{1}{2}\left(50^0+90^0\right)=70^0\)
ΔIMK cân tại I
=>\(\widehat{KIM}=180^0-2\cdot70^0=40^0\)

1: sđ cung DE=50 độ
=>góc DOE=50 độ
=>góc DCE=50/2=25 độ; góc BOE=90-50=40 độ
2: Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
Xét tứ giác IODE có
góc IOD+góc IED=180 độ
=>IODE là tứ giác nội tiếp