K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
YT
25 tháng 3 2018
a<b
suy ra-4a<-4b
suy ra2016-4a<2016-4b
ma 2016-4b<2017-4b
vay 2016-4a,<2017-4b
25 tháng 3 2018
Ta có: a > b
khi nhân cả 2 vế vs -4
=> -4a < -4b
Cộng cả 2 vế với 2016:
=> 2016 - 4a < 2016 - 4b (1)
Ta có: 2016 < 2017
Khi Cộng cả 2 vế vs -4b
=> 2016 - 4b < 2017 - 4b (2)
Từ (1) và (2) => 2016 - 4a < 2017 - 4b
NN
24 tháng 4 2019
a) Ta có: a>b => 2a > 2b (nhân 2 vế với 2)
=> 2a - 3 > 2b - 3 (cộng 2 vế với -3)
b) Ta có: -4a+1 < -4b+ 1 => -4a < -4b ( cộng 2 vế với -1)
=> a > b (nhân 2 vế với -1/4)
c) Ta có: 3-4a < 5c+2 => 3-4a-3 < 5c+2-3 (cộng 2 vế với -3)
=> -4a < 5c-1
Mà 5c-1 < -4b nên -4a < -4b => a > b (nhân cả 2 vế với -1/4)
25 tháng 5 2022
tham khảo
4a + 5 < 4b+5
<=> 4a +5 - 5 < 4b+5 - 5
<=> 4a < 4b
<=> a < b
MP
24 tháng 4 2023
1.
a. -3a - 1 + 1 > -3b - 1 + 1 (cộng cả 2 vế cho 1)
-3a . \(\left(\dfrac{-1}{3}\right)\) < -3b . \(\left(\dfrac{-1}{3}\right)\) (nhân cả vế cho \(\dfrac{-1}{3}\) )
a < b
b. 4a + 3 + (- 3) < 4b + 3 +(- 3) (cộng cả 2 vế cho -3)
4a . \(\dfrac{1}{4}\) < 4b . \(\dfrac{1}{4}\) (nhân cả 2 vế cho \(\dfrac{1}{4}\) )
a < b
2.
a. Ta có: a < b
3a < 3b ( nhân cả 2 vế cho 3)
3a - 7 < 3b - 7 (cộng cả 2 vế cho - 7 )
b. Ta có: a < b
-2a > -2b (nhân cả 2 vế cho -2)
5 - 2a > 5 - 2b ( cộng cẩ 2 vế cho 5)
c. Ta có: a < b
2a < 2b (nhân cả vế cho 2)
2a + 3 < 2b + 3 (cộng cả 2 vế cho 3)
d. Ta có: a < b
3a < 3b (nhân cả 2 vế cho 3)
3a - 4 < 3b - 4 (cộng cả 2 vế cho -4)
Ta có: 3 < 4
đến đây ko bắt cầu qua đc chắc đề bài sai
12 tháng 2 2021
Ta có: \(C=\dfrac{2019-2018}{2019+2018}\)
\(\Leftrightarrow C=\dfrac{\left(2019-2018\right)\left(2019+2018\right)}{\left(2019+2018\right)^2}\)
\(\Leftrightarrow C=\dfrac{2019^2-2018^2}{\left(2019+2018\right)^2}\)
Ta có: \(\left(2019+2018\right)^2=2019^2+2018^2+2\cdot2019\cdot2018\)
\(2019^2+2018^2=2019^2+2018^2+0\)
Do đó: \(\left(2019+2018\right)^2>2019^2+2018^2\)
\(\Leftrightarrow\dfrac{2019^2-2018^2}{\left(2019+2018\right)^2}< \dfrac{2019^2-2018^2}{2019^2+2018^2}\)
\(\Leftrightarrow C< D\)
HP
1
19 tháng 4 2023
b: a>b
=>-4a<-4b
=>-4a+7<-4b+7
a: TH1: x>=2
=>2x-4=3-3x
=>5x=7
=>x=7/5(loại)
TH2: x<2
=>4-2x=3-3x
=>x=-1(nhận)
RZ
1
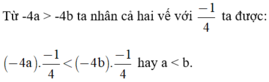
-4a2018<-4b2019 vì số âm có giá trị tuyệt đối càng lớn thì càng nhỏ nhé
`a>b`
`<=>-a<-b`
`<=>-4a<-4b`
`<=>-4a-2018<-4b-2018<-4b-2019`