K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KV
22 tháng 10 2023
a) P = 1 + 3 + 3² + ... + 3¹⁰¹
= (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)
= 13 + 3³.(1 + 3 + 3²) + ... + 3⁹⁹.(1 + 3 + 3²)
= 13 + 3³.13 + ... + 3⁹⁹.13
= 13.(1 + 3³ + ... + 3⁹⁹) ⋮ 13
Vậy P ⋮ 13
b) B = 1 + 2² + 2⁴ + ... + 2²⁰²⁰
= (1 + 2² + 2⁴) + (2⁶ + 2⁸ + 2¹⁰) + ... + (2²⁰¹⁶ + 2²⁰¹⁸ + 2²⁰²⁰)
= 21 + 2⁶.(1 + 2² + 2⁴) + ... + 2²⁰¹⁶.(1 + 2² + 2⁴)
= 21 + 2⁶.21 + ... + 2²⁰¹⁶.21
= 21.(1 + 2⁶ + ... + 2²⁰¹⁶) ⋮ 21
Vậy B ⋮ 21
c) A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... + 2¹⁶) ⋮ 5
Vậy A ⋮ 5
d) A = 1 + 4 + 4² + ... + 4⁹⁸
= (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + ... + (4⁹⁷ + 4⁹⁸ + 4⁹⁹)
= 21 + 4³.(1 + 4 + 4²) + ... + 4⁹⁷.(1 + 4 + 4²)
= 21 + 4³.21 + ... + 4⁹⁷.21
= 21.(1 + 4³ + ... + 4⁹⁷) ⋮ 21
Vậy A ⋮ 21
e) A = 11⁹ + 11⁸ + 11⁷ + ... + 11 + 1
= (11⁹ + 11⁸ + 11⁷ + 11⁶ + 11⁵) + (11⁴ + 11³ + 11² + 11 + 1)
= 11⁵.(11⁴ + 11³ + 11² + 11 + 1) + 16105
= 11⁵.16105 + 16105
= 16105.(11⁵ + 1)
= 5.3221.(11⁵ + 1) ⋮ 5
Vậy A ⋮ 5
PT
1
CM
29 tháng 3 2017
Ta có: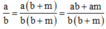 
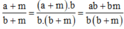
Ta có: a/b > 1 nên a > b suy ra am > bm, suy ra ab + am > ab + bm.
Do đó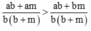 
Hay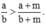 
TP
2
24 tháng 7 2016
Do a(a + 1) là tích 2 số nguyên liên tiếp => a(a - 1) chia hết cho 2
+ Nếu a và b cùng lẻ hoặc cùng chẵn thì a + b chia hết cho 2 => ab(a + b) chia hết cho 2
+ Nếu trong 2 số a và b có 1 số chẵn, 1 số lẻ => a hoặc b chia hết cho 2 => ab(a + b) chia hết cho 2
=> a(a + 1) - ab(a + b) luôn chia hết cho 2
DS
24 tháng 7 2016
Theo toán suy luận nói thì thế này:
a và a+1 là 2 số nguyên liên tiếp nên 1 số sẽ chia hết cho 2.
Nếu a chẵn thì ab(a+b) chia hết cho 2.
Còn trường hợp a lẻ và b cũng lẻ(b chẵn cũng chia hết cho 2):
a+b luôn chia hết cho 2.
Vậy a(a+1)-ab(a+b) chia hết cho 2.
Chúc em học tốt^^
CM
7 tháng 9 2019
a) Thực hiện quy đồng a b = a ( b + m ) b ( b + m ) = a b + a m b 2 + b m ;
a + m b + m = b ( a + m ) b ( b + m ) = a b + b m b 2 + b m . Vì a b < 1=> a < b => ab +am < ab + bm
Từ đó thu được a b < a + m b + m
b) 437 564 < 437 + 9 564 + 9 = 446 573 .
TQ
2
13 tháng 3 2020
a(a+1) luôn chia hết cho 2 nên cần cm ab(a+b) chia hết cho 2
xét a chia hết cho 2,b ko chia hết
\(\Rightarrow\)ab(a+b) chia hết cho 2
xét a ko chia hết cho 2,b chia hết cho 2\(\Rightarrow\)ab(a+b) chia hết cho 2
xét a,b ko chia hết cho 2\(\Rightarrow\hept{\begin{cases}a=2k+1\\b=2l+1\end{cases}\Rightarrow a+b=2k+2l+2⋮2}\)
\(\Rightarrow a+b⋮2\Rightarrow ab\left(a+b\right)⋮2\left(đpcm\right)\)
CX
13 tháng 3 2020
Xét : a.(a +1) thì sẽ có một số là số chẵn mà số chẵn chia hết cho 2
=) a.(a +1)\(⋮\)2 ( 1 )
Xét : ab .(a+b)
ta có : (a+b) chỉ có 1 trường hợp là số lẻ duy nhất khi a và b không cùng tính chất chẵn / lẻ
các TH còn lại thì (a+b)\(⋮\) 2 nên ab .(a+b)
nếu (a+b) lẻ thì a.b chẵn vì một trong a và b là số chẵn ( 2 )
Từ (1) và (2) =) ( đpcm )
đăng kí kênh của V-I-S nha !
17 tháng 6 2016
Từ AB=BC=CA
suy ra: AB+BC=2CA > CA
BC + AC = 2AB > AB
AB+AC = 2BC > BC
Suy ra A,B,C là 3 đỉnh của 1 tam giác vì nó thỏa mãn tính chất: Tổng 2 cạnh lớn hơn cạnh còn lại.
VT
0
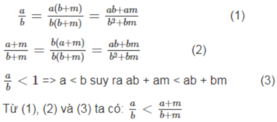
Gọi d là \(\left(ƯC_{ab;a+b}\right)\) Theo đề bài ra ta có:
\(ab⋮d\)
\(\Rightarrow\)a hoặc b đều chia hết cho d
mà a+b chia hết cho d
\(\Rightarrow a;b\)đều chia hết cho d
\(\Rightarrow\left(a;b\right)>1\)(trái giả thuyết)
\(\Rightarrow\left(ab;a+b\right)⋮d\) (đpcm)