Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trước tiên, ta xác định tập hợp B\A: B\A là tập hợp các phần tử thuộc tập B mà không thuộc tập A. Tập A chứa các giá trị x thỏa mãn |mx-3|=mx-3. Điều này có nghĩa là ta cần tìm các giá trị x mà khi thay vào phương trình trên, phương trình vẫn đúng.
Tiếp theo, ta xác định tập hợp B: B là tập hợp các giá trị x thỏa mãn x^2-2x-4=0. Để giải phương trình này, ta có thể sử dụng công thức nghiệm của phương trình bậc 2, hoặc sử dụng định lý Viết.
Giải phương trình x^2-2x-4=0 bằng cách sử dụng công thức nghiệm của phương trình bậc 2, ta có: x = (2 ± √(2^2 - 41(-4))) / (2*1) = (2 ± √(4 + 16)) / 2 = (2 ± √20) / 2 = 1 ± √5
Vậy tập hợp B là B = {1 + √5, 1 - √5}.
Cuối cùng, ta xác định tập hợp B\A: B\A là tập hợp các phần tử thuộc tập B mà không thuộc tập A. Điều này có nghĩa là ta cần loại bỏ các giá trị x thuộc tập A khỏi tập B.
Từ phương trình |mx-3|=mx-3, ta có hai trường hợp để xác định tập A:
Khi mx-3 > 0, ta có mx-3 = mx-3, điều này đúng với mọi giá trị x.Khi mx-3 < 0, ta có -(mx-3) = mx-3, điều này đúng khi mx > 3.Với mọi giá trị x thỏa mãn mx > 3, ta có x thuộc tập A.
Vậy tập hợp B\A = B - A = {1 + √5, 1 - √5} - {x | mx > 3}.
Để tìm m sao cho B\A = B, ta cần tìm giá trị m mà tập hợp B\A bằng tập hợp B. Tức là, ta cần giải phương trình sau: {1 + √5, 1 - √5} - {x | mx > 3} = {1 + √5, 1 - √5}.
Điều này xảy ra khi và chỉ khi tập hợp {x | mx > 3} không chứa bất kỳ giá trị nào từ tập hợp {1 + √5, 1 - √5}. Nghĩa là không có giá trị x thỏa mãn mx > 3 và x thuộc {1 + √5, 1 - √5}.
Vì vậy, để B\A = B, ta cần tìm giá trị m sao cho không có giá trị x thuộc {1 + √5, 1 - √5} thỏa mãn mx > 3.
Tuy nhiên, không có giá trị m nào thỏa mãn yêu cầu trên vì tập hợp {1 + √5, 1 - √5} chứa cả hai giá trị x lớn hơn 3 và nhỏ hơn 3.
Vậy không tồn tại giá trị m để B\A = B.

\(\left|mx-3\right|=mx-3\Leftrightarrow mx-3\ge0\) \(\Rightarrow\left[{}\begin{matrix}x\ge\dfrac{3}{m}\left(m>0\right)\\x\le\dfrac{3}{m}\left(m< 0\right)\end{matrix}\right.\)
\(x^2-4=0\Rightarrow x=\pm2\Rightarrow B=\left\{-2;2\right\}\)
\(B\backslash A=B\Leftrightarrow A\cap B=\varnothing\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{3}{m}>2\left(m>0\right)\\\dfrac{3}{m}< -2\left(m< 0\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}0< m< \dfrac{3}{2}\\-\dfrac{3}{2}< m< 0\end{matrix}\right.\)

Cái này mình không biết cách trình bày
Nhưng mình nghĩ cách giải sẽ như này: Đầu tiên bạn tìm x trước rồi thay vào pt trong A để tìm m

tthTrần Thanh PhươngVũ Minh TuấnLightning Farron
Nguyễn Văn ĐạtLê Thị Thục HiềnAkai Haruma



\(B=\left\{x\in R|x^2-4=0\right\}=\left\{2;-2\right\}\)
Điều kiện B∖A=B nếu
Với x = 2 ta có: 2m<3 => \(m< \frac{3}{2}\)
Với x = -2 ta có: -2m < 3 => \(m>-\frac{3}{2}\)
=> \(-\frac{3}{2}< m< \frac{3}{2}\)
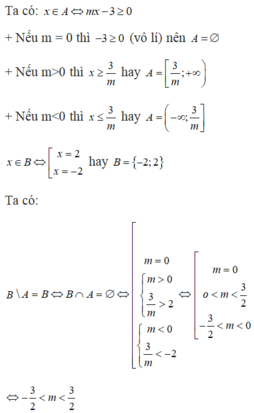
B={2;-2}
mx-3=mx-3
=>0mx=0
=>\(x\in R\)
=>A=R
B\A=B khi B giao A bằng rỗng
=>m<>2 và m<>-2