Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)
=>\(\left\{{}\begin{matrix}m-1>2\\m+3\le5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>3\\m\le2\end{matrix}\right.\)(vô lý)
vậy ko tồn tại m

a: \(A\cap B=\left(-3;1\right)\)
\(A\cup B\)=[-5;4]
A\B=[1;4]
\(C_RA\)=R\A=(-∞;-3]\(\cap\)(4;+∞)
b: C={1;-1;5;-5}
\(B\cap C=\left\{-5;-1\right\}\)
Các tập con là ∅; {-5}; {-1}; {-5;-1}

a, \(A\subset B\Leftrightarrow\left\{{}\begin{matrix}m+3\ge5\\2m-1< -4\end{matrix}\right.\Rightarrow m\in\left\{\varnothing\right\}\)
b, \(B\subset A\Leftrightarrow\left\{{}\begin{matrix}m+3\le5\\2m-1>-4\end{matrix}\right.\Leftrightarrow-\dfrac{3}{2}< m\le2\)
c, \(A\cap B=\varnothing\Leftrightarrow\left[{}\begin{matrix}2m-1>5\\m+3\le-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m>3\\m\le-7\end{matrix}\right.\)
d, \(A\cup B\) là một khoảng \(\Leftrightarrow\left\{{}\begin{matrix}m+3>5\\2m-1\le5\end{matrix}\right.\Leftrightarrow2< m\le3\)

Bài 1:
Để A giao B bằng rỗng thì \(\left[{}\begin{matrix}m+3< -3\\2m-1>6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m< -6\\m>\dfrac{7}{2}\end{matrix}\right.\)

a/
\(\Leftrightarrow2m+3\ge m+1\Leftrightarrow m\ge-2\)
b/
Tổng 3 phần tử chẵn \(\Rightarrow\) có các trường hợp:
- Cả 3 phần tử đều chẵn: có đúng 1 tập \(\left\{2;4;6\right\}\)
- 2 phần tử lẻ và 1 phần tử chẵn: chọn 2 phần tử lẻ từ 3 phần tử lẻ có 3 cách, kết hợp với 1 trong 3 phần tử chẵn \(\Rightarrow3.3=9\) tập
Vậy có 10 tập thỏa mãn

Để A hợp B=A thì B là tập con của A
=>2m-5<23 và 23<=-m
=>2m<28 và -m>=23
=>m<=-23 và m<14
=>m<=-23
=>Chọn B

Tham khảo:
a) \(A \subset A \cup B\) vì
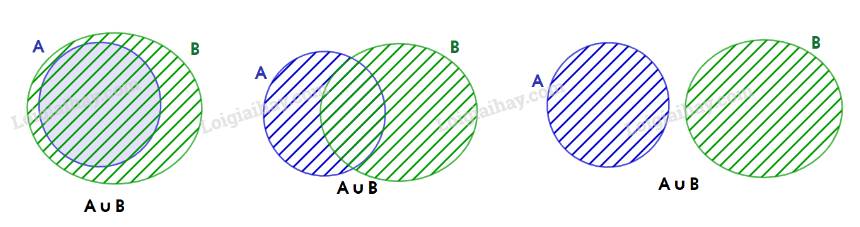
b) \(A \cap B \subset A\) vì
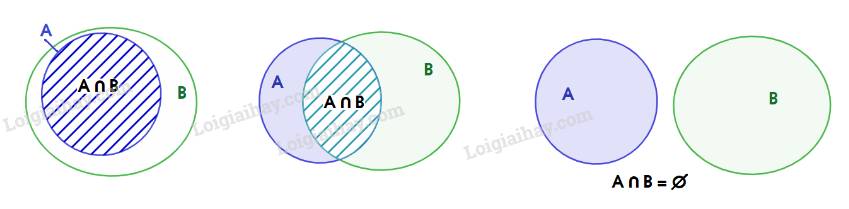

Lời giải:
$A\cap B\cap C=A\cap (B\cap C)$
Để tập hợp trên khác rỗng thì trước hết $B\cap C\neq \varnothing$
Điều này xảy ra khi $2m>m\Leftrightarrow m>0$
Khi đó: $B\cap C=(m; 2m)$
$\Rightarrow A\cap B\cap C=((-3;-1)\cup (1;2))\cap (m; 2m)$
$=((-3;-1)\cap (m;2m))\cup ((1;2)\cap (m; 2m))$
$=(1;2)\cap (m; 2m)$ (do $m>0$)
Để $(1;2)\cap (m; 2m)\neq \varnothing$ thì:
\(\left\{\begin{matrix} 2m>1\\ m< 2\end{matrix}\right.\Leftrightarrow m\in (\frac{1}{2};2)\)
Vậy...........

\(A=\left(-3;-1\right)\cup\left(1;2\right)\)
\(B=\left(-1;+\infty\right)\)
\(C=\left(-\infty;2m\right)\)
\(A\cap B=\left(-3;-1\right)\)
Để \(A\cap B\cap C\ne\varnothing\Leftrightarrow2m\ge-1\)
\(\Leftrightarrow m\ge-\dfrac{1}{2}\)
Vậy \(m\ge-\dfrac{1}{2}\) thỏa đề bài
a) để \(A\subset B\Leftrightarrow\left\{{}\begin{matrix}2m-1\ge-4\\m+3\le5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ge\dfrac{-3}{2}\\m\le2\end{matrix}\right.\Leftrightarrow\dfrac{-3}{2}\le m\le2\)
b) để \(B\subset A\Leftrightarrow\left\{{}\begin{matrix}2m-1\le-4\\m+3\ge5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\le\dfrac{-3}{2}\\m\ge2\end{matrix}\right.\Rightarrow m\in\varnothing\)
c) để \(A\cap B=\varnothing\Leftrightarrow\left[{}\begin{matrix}m+3< 4\\5< 2m-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m< 1\\m>3\end{matrix}\right.\)
\(\Rightarrow m\in\left(-\infty;1\right)\cup\left(3;+\infty\right)\)
cho mình hỏi câu c.
tại sao m+3< 4 mà ko phải m+3<-4