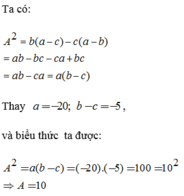Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A = b ( a - c ) - c ( a - b )
A = ab - bc - ac + bc
A = ab - ac = a ( b - c )
A = - 20 . ( - 5 ) = 100 = 102 = ( - 10 )2
Ta có:
A = b(a - c) - c(a - b)
A = ab - cb - ac - cb
A = ab - ac
A = a(b - c)
A = (-20)(-5)
A = 100
Vậy...

Bài làm:
Ta có: \(A^2=b\left(a-c\right)-c\left(a-b\right)\)
\(A^2=ab-bc-ac+bc\)
\(A^2=ab-ac=a\left(b-c\right)\)
\(A^2=\left(-5\right).\left(-20\right)=100\)
\(\Rightarrow\orbr{\begin{cases}A=10\\A=-10\end{cases}}\)

Ta có:
A 2 = b ( a − c ) − c ( a − b ) = ab − bc − ca + bc = ab − ca = a ( b − c )
Thay a = -20, b - c = -5 vào biểu thức ta được:
A 2 = a ( b − c ) = ( − 20 ) . ( − 5 ) = 100 = 10 2 ⇒ A = 10

Sửa đề nhé , đề sai :
\(\text{Ta có : }A=b\left(a-c\right)-c\left(a+b\right)\)
\(\Leftrightarrow A=ba-bc-ca-cb\)
\(\Leftrightarrow A=ab-ca\)
\(\Leftrightarrow A=a\left(b-c\right)\)
\(\Leftrightarrow A=\left(-20\right)\left(-5\right)\)
\(\Rightarrow A=100\)

\(2x^4-x^3+2x^2+1=2x^4-2x^3+2x^2+x^3-x^2+x+x^2-x+1\\ \)
\(=2x^2\left(x^2-x+1\right)+x\left(x^2-x+1\right)+\left(x^2-x+1\right)=\left(x^2-x+1\right)\left(2x^2+x+1\right)\)
Vậy a = 2; b = 1; c = 1.

Lời giải:
Giả sử $(a^2+b^2, ab)>1$. Khi đó, gọi $p$ là ước nguyên tố lớn nhất của $(a^2+b^2,ab)$
$\Rightarrow a^2+b^2\vdots p; ab\vdots p$
Vì $ab\vdots p\Rightarrow a\vdots p$ hoặc $b\vdots p$
Nếu $a\vdots p$. Kết hợp $a^2+b^2\vdots p\Rightarrow b^2\vdots p$
$\Rightarrow b\vdots p$
$\Rightarrow p=ƯC(a,b)$ . Mà $(a,b)=1$ nên vô lý
Tương tự nếu $b\vdots p$
Vậy điều giả sử là sai. Tức là $(a^2+b^2, ab)=1$