Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
a) Ta có: \(C=2+2^2+2^3+...+2^{99}+2^{100}\)
\(=\left(2+2^2+2^3+2^4+2^5\right)+\left(2^6+2^7+2^8+2^9+2^{10}\right)+...+\left(2^{96}+2^{97}+2^{98}+2^{99}+2^{100}\right)\)
\(=2\left(1+2+2^2+2^3+2^4\right)+2^6\left(1+2+2^2+2^3+2^4\right)+...+2^{96}\left(1+2+2^2+2^3+2^4\right)\)
\(=31\cdot\left(2+2^6+...+2^{96}\right)⋮31\)(đpcm)
Bài 1:
Ta có: \(A=3^{n+2}-2^{n+2}+3^n-2^n\)
\(=3^n\cdot9-2^n\cdot4+3^n-2^n\)
\(=3^n\left(9+1\right)-2^n\left(4+1\right)\)
\(=10\left(3^n-2^{n-1}\right)⋮10\)
Vậy: A có chữ số tận cùng là 0
Bài 2:
Ta có: \(abcd=1000\cdot a+100\cdot b+10\cdot c+d\)
\(\Leftrightarrow abcd=1000\cdot a+96\cdot b+8c+2c+4b+d\)
\(\Leftrightarrow abcd=8\left(125a+12b+c\right)+\left(2c+4b+d\right)\)
mà \(8\left(125a+12b+c\right)⋮8\)
và \(2c+4b+d⋮8\)
nên \(abcd⋮8\)(đpcm)

Lời giải:
$S=(2+2^2)+(2^3+2^4)+....+(2^{23}+2^{24})$
$=2(1+2)+2^3(1+2)+....+2^{23}(1+2)$
$=(1+2)(2+2^3+...+2^{23})$
$=3(2+2^3+...+2^{23})\vdots 3$
b.
$S=2+2^2+2^3+...+2^{23}+2^{24}$
$2S=2^2+2^3+2^4+....+2^{24}+2^{25}$
$\Rightarrow 2S-S=2^{25}-2$
$\Rightarrow S=2^{25}-2$
Ta có:
$2^{10}=1024=10k+4$
$\Rightarrow 2^{25}-2=2^5.2^{20}-2=32(10k+4)^2-2=32(100k^2+80k+16)-2$
$=10(320k^2+8k+51)\vdots 10$
$\Rightarrow S$ tận cùng là $0$

A=2+22+23+...+220A=2+22+23+...+220
2A=22+23+24+...+2212A=22+23+24+...+221
2A−A=(22+23+24+...+221)−(2+22+23+...+220)2A−A=(22+23+24+...+221)−(2+22+23+...+220)
A=221−2=24.5+1−2=(24)5.2−2=165.2−2A=221−2=24.5+1−2=(24)5.2−2=165.2−2
A=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯.......6.2−2=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯........2−2=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯...........0A=.......6¯.2−2=........2¯−2=...........0¯
Vậy chữ số tận cùng cả A là 0

a) Tổng A có số số hạng là:
`(101-1):1+1=101`(số hạng)
b) `A=2+2^3 +2^5 +...+2^101`
`2^2 A=2^3 +2^5 +2^7 +...+2^103`
`4A-A=2^3 +2^5 +2^7 +...+2^103 -2-2^3 -2^5 -...-2^101`
`3A=2^103 -2`
`=>3A+2=2^103 -2+2=2^103`
c) `A=2+2^3 +2^5 +...+2^101`
`A=2(1+2^2 +2^4 +...+2^100)⋮2`
`A=2+2^3 +2^5 +...+2^101`
`A=2(1+2^2 +2^4)+...+2^97 .(1+2^2 +2^4)`
`A=2.21+...+2^97 .21`
`A=21(2+...+2^97)⋮21`

a) Ta có: \(A=4+4^2+4^3+....+4^{24}\)
\(\Rightarrow A=\left(4+4^2+4^3\right)+....+\left(4^{22}+4^{23}+4^{24}\right)\)
\(\Rightarrow A=4.\left(1+4+4^2\right)+....+4^{22}.\left(1+4+4^2\right)\)
\(\Rightarrow A=21.\left(4+....+4^{22}\right)⋮21\)
Vậy \(A⋮21\)
b) Tự làm

Chia hết cho 3
a) A = 2 + 22 + 23 +....... + 2100
A = ( 2+ 22) + (23 + 24) + ........ (299+2100)
A = 2(1+2) + 23(1+2) + ........+ 299(1+2)
A= 2. 3 + 23 . 3 + ........ + 299. 3
= 3 . ( 2 + 23 + .........+ 299)
Vì 3 chia hết cho 3 => 3. ( 2 + 23 + ........+299) chia hết cho 3 hay A chia hết cho 3
Chia hết cho 15 cũng tương tự như vậy nha bn!
Ghép 4 số rồi tính!
CHÚC BN HOK GIỎI!


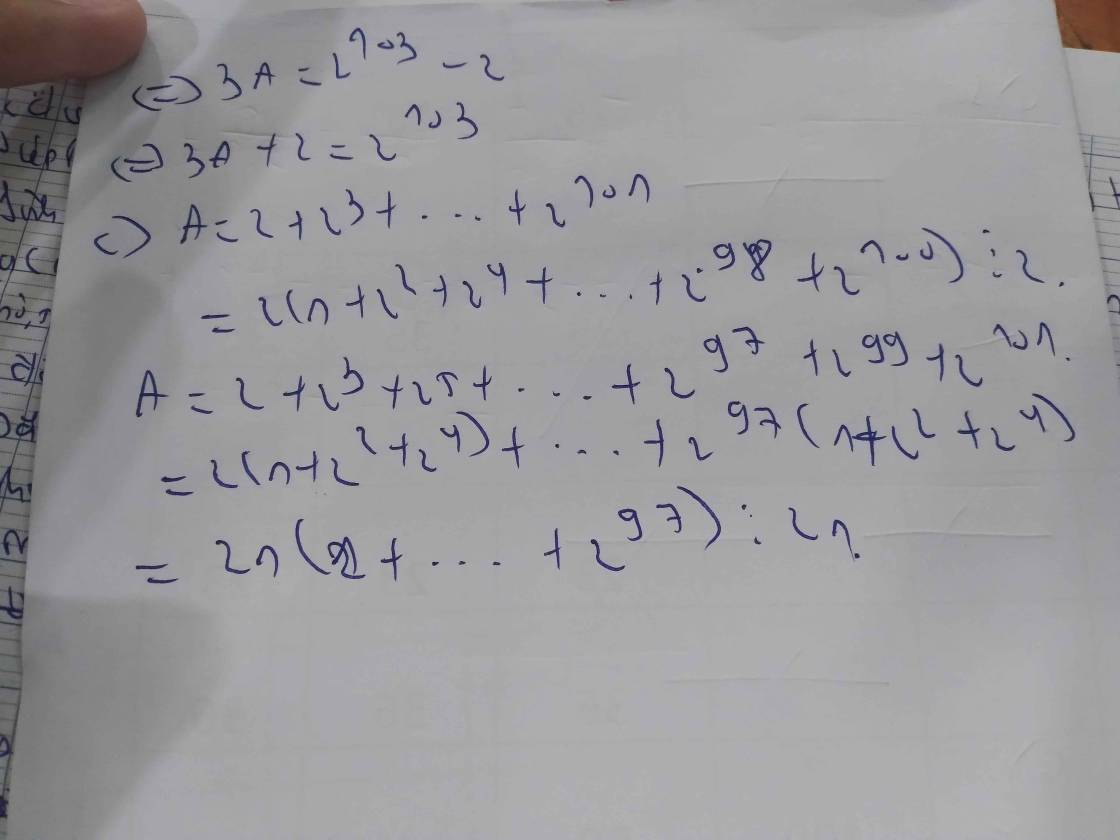
a) Có A=2+22+23+24+...+2100
= 2.(1+2+4+8)+25.(1+2+4+8)+29(1+2+4+8)+...+296.(1+2+4+8)
=2.15+25.15+29.15+...+296.15
=15(2+25+29+...+296)
=> A \(⋮\) 15
b)
A=2+22+23+.....+2100
= (2 + 22 + 23 + 24) + .... + (297 + 298 + 299 + 2100)
= 1.30 + 24.30 + ..... + 296.30
= 30.(1+34+...+296)
=>A\(⋮\) 30 < = > A \(⋮\) 10
< = >A có tận cùng là 0