Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Chia tập A theo số dư khi chia cho 3 ta có: ![]()
Chọn chữ số hàng đầu tiên có: 5 cách
Chọn 3 chữ số3 hàng tiếp theo có: 6 3 cách
Chọn chữ số hàng cuối cùng có 2 cách vì...
Nếu tổng của 4 số đã chọn chia 3 dư 0 thì chọn số cuối ở tập {0;3}
Chọn chữ số hàng cuối cùng có 2 cách vì...
Nếu tổng của 4 số đã chọn chia 3 dư 0 thì chọn số cuối ở tập {2;5}
Nếu tổng của 4 số đã chọn chia 3 dư 2 thì chọn số cuối ở tập {1;4}
Trường hợp nào cũng chỉ có 2 lựa chọn.
Đáp số: ![]()

Đáp án B
Chia tập A theo số dư khi chia cho 3 ta có: A = 0 , 3 ∪ 1 , 4 ∪ 2 , 5
Chọn chữ số hàng đầu tiên có:5 cách
Chọn 3 chữ số 3 hàng tiếp theo có: 6 3 cách
Chọn chữ số hàng cuối cùng có 2 cách vì...
Nếu tổng của 4 số đã chọn chia 3 dư 0 thì chọn số cuối ở tập {0,3}
Nếu tổng của 4 số đã chọn chia3 dư 1 thì chọn số cuối ở tập {2,5}
Nếu tổng của 4 số đã chọn chia 3 dư 2 thì chọn số cuối ở tập {1,4}
Trường hợp nào cũng chỉ có 2 lựa chọn.
Đáp số: 5 .6 3 . 2 = 2160

Đáp án B
Số các số có chín chữ số khác nhau là 9!. Trong 9! số này, số các số mà chữ số 1 đứng trước chữ số 2 hoặc chữ số 1 đứng sau chữ số 2 là bằng nhau. Do đó, số các số mà chữ số 1 đứng trước chữ số 2 là 9 ! 2 .
Tương tự, số các số mà chữ số 1 đứng trước chữ số 2 và chữ số 3 đứng trước chữ số 4 là 9 ! 4 .
Số các số cần tìm là 9 ! 8 = 45360.

Gọi số tự nhiên cần lập có dạng a b c d ¯ a , b , c , d ∈ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 .
Số cần lập chia hết cho 15 nên nó chia hết cho 3 và 5.
Số cần lập chia hết cho 5 nên ta có: d = 5 ⇒ d có 1 cách chọn.
Số cần tìm có dạng: a b c 5 ¯ .
Số cần lập chia hết cho 3 nên a + b + c + 5 : 3 .
Chọn a có 9 cách chọn, chọn b có 9 cách chọn.

Có 3 cách chọn c.
Như vậy có: 9.9.3.1 = 243 cách chọn.
Vậy có 243 số thỏa mãn yêu cầu bài toán.
Chọn D.

Tập S có 9 4 phần tử. Ta có
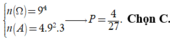
Thật vậy: Gọi số thỏa mãn biến cố là ![]()
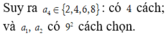
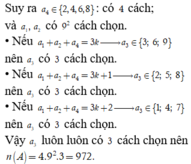




Chọn C
Gọi số cần tìm là a = a 1 a 2 a 3 a 4 a 5 ¯ a i ≠ 0 Do a ⋮ 3 nên a 1 + a 2 + a 3 + a 4 + a 5 ⋮ 3
Nếu a 1 + a 2 + a 3 + a 4 ⋮ thì a 5 = 0 hoặc a 5 = 3
Nếu a 1 + a 2 + a 3 + a 4 chia 3 dư 1 thì a 5 = 2 hoặc a 5 = 5 .
Nếu a 1 + a 2 + a 3 + a 4 chia 3 dư 2 thì a 5 = 1 hoặc a 5 = 4 .
Như vậy, từ một số có 4 chữ số a 1 a 2 a 3 a 4 (các số được lấy từ tập A) sẽ tạo được 2 số tự nhiên có 5 chữ số thỏa mãn yêu cầu bài toán.
Dễ thấy từ các chữ số của tập A có thể lập được 5.6.6.6 = 1080 số tự nhiên có 4 chữ số.
Do đó từ các chữ số của tập A sẽ lập được 2.1080 = 2160 số chia hết cho 3 có 5 chữ số.