
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bn cop lên mạng đề này vào trang đầu tiên là có đấy
Tick cho mik nhé![]()
Ta có:\(a^3+b^3+c^3-a-b-c\)
\(=a\left(a^2-1\right)+b\left(b^2-1\right)+c\left(c^2-1\right)\)
\(=a\left(a-1\right)\left(a+1\right)+b\left(b-1\right)\left(b+1\right)+c\left(c-1\right)\left(c+1\right)\)
Mà \(a\left(a-1\right)\left(a+1\right),b\left(b-1\right)\left(b+1\right),c\left(c-1\right)\left(c+1\right)\)là tích 3 số nguyên liên tiếp
\(\Rightarrow\)\(a\left(a-1\right)\left(a+1\right)⋮3,b\left(b-1\right)\left(b+1\right)⋮3,c\left(c-1\right)\left(c+1\right)⋮3\)
\(\Rightarrow a\left(a-1\right)\left(a+1\right)+b\left(b-1\right)\left(b+1\right)+c\left(c-1\right)\left(c+1\right)⋮3\)Mà \(a+b+c⋮3\Rightarrow a^3+b^3+c^3⋮3\)

\(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\left(a^3+3a^2b+3ab^2+b^3\right)+c^3-3abc-3a^2b-3ab^2=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3abc\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ac-bc-ab\right)=0\)
\(\Leftrightarrow\frac{1}{2}\left(a+b+c\right)\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]=0\)
Vì a;b;c đôi 1 khác nhau nên \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ne0\)
\(\Rightarrow a+b+c=0\) (đpcm)
chuyển vế -> phân tích a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ca) -> cm a2+b2+c2-ab-bc-ca >= 0
ta có: a2+b2+c2-ab-bc-ca >= 0 <=> 2a2+2b2+2c2-2ab-2bc-2ca >= 0 <=> (a2-2ab+b2)+(b2-2bc+c2)+(c2-2ca+a2) >=0
<=>(a-b)2+(b-c)2+(c-a)2 >=0
dấu "=" xảy ra khi a=b=c mà a,b,c đôi một khác nhau => a2+b2+c2-ab-bc-ca khác 0 <=> a+b+c=0

Bài này cần dùng một ít kiến thức của lớp 8, bạn có thể tìm hiểu thêm.
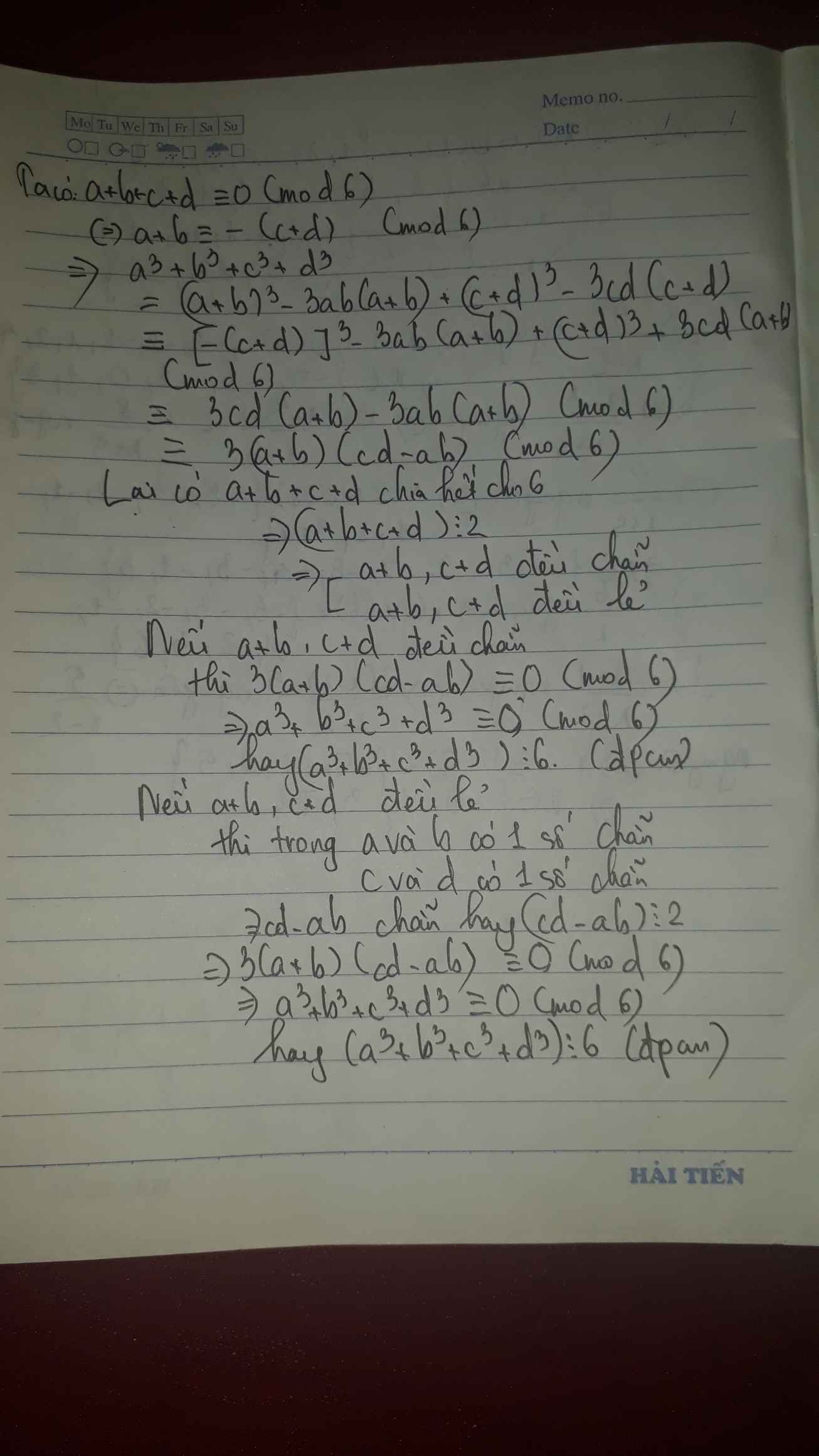
a^3 + b^3 + c^3 - 3 abc = ( a + b) ^3 - 3ab( a+b) + c^3 - 3abc
= ( a +b +c )^3 - 3( a+b)^2.c - 3(a+b).c^2 - 3ab ( a+b+c)
= ( a+b + c)^3 - 3(a+b).c (a+ b +c) - 3ab(a+b+c)
= (a+ b+ c) [ (a+ b+ c)^2 - 3(a+b).c - 3ab)] chia hết cho a + b +c