Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

OM là tia phân giác của \(\widehat{AOC}\left(gt\right)\Rightarrow\widehat{AOM}=\widehat{MOC}\)
Ta có: \(\widehat{AOM}+\widehat{MON}+\widehat{NOB}=180^0\)
\(\Rightarrow\widehat{AOM}+\widehat{NOB}=90^0\)(1)
Vì tia OC nằm giữa 2 tia OM,ON nên: \(\widehat{MOC}+\widehat{CON}=\widehat{MON}\)
\(\Rightarrow\widehat{AOM}+\widehat{CON}=90^0\)(2)
Từ (1) và (2), ta có: \(\widehat{BON}=\widehat{CON}\)
Mà tia ON nằm giữa 2 tia OB,OC
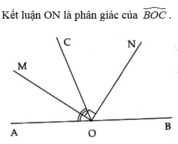
Nên ON là tia phân giác của \(\widehat{BOC}\)

Vì OM là tia phân giác của góc AOB nên :
Góc AOM = góc MBO
Ta có góc BOM + Góc BON = góc MON = 90 độ
Góc AOC = 180 độ ( góc bẹt )
=> Góc AOC - góc MON = góc MOA + Góc NOC
Mà móc MOA = góc BOM nên :
=> góc BON = góc CON
hay ON là phân chia giác của góc BOC
Chú ý : Đây là vì sao nha !!!
Và mk lớp 6 :3

Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.

Bài làm
Ta có: \(\widehat{AOC}+\widehat{COB}=180^0\)( hai góc kề bù )
Hay \(\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}=180^0\)
Mà \(\widehat{O_2}+\widehat{O_3}=90^0\)
=> \(\widehat{O_1}+90^0+\widehat{O_4}=180^0\)
=> \(\widehat{O_1}+\widehat{O_4}=180^0-90^0\)
=> \(\widehat{O_1}+\widehat{O_4}=90^0\)
Lại có \(\widehat{O_1}=\widehat{O_2}\)
=> \(\widehat{O_2}+\widehat{O_4}=90^0\)
Mà \(\widehat{O_2}+\widehat{O_3}=90^0\)
=> \(\widehat{O_4}=\widehat{O_3}\)
=> ON là tia phân giác của \(\widehat{COB}\)
Vậy ON là tia phân giác của \(\widehat{COB}\)
# Học tốt #