Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

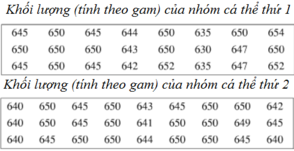
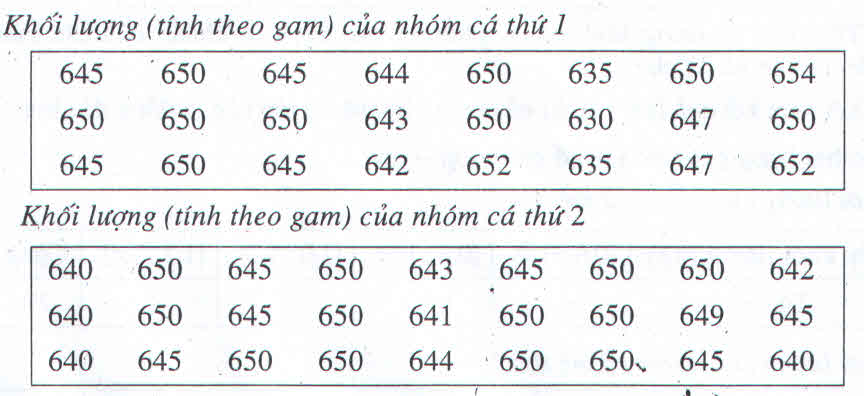
Dựa vào bảng phân dữ liệu đề bài cho ta có bảng phân bố tần số ;tần suất như sau:
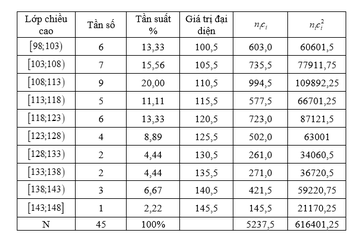
Số trung bình cộng của bảng số liệu:
![]()
Chọn B

Chọn B
Dựa vào bảng phân dữ liệu đề bài cho ta có bảng phân bố tần số, tần suất như sau:
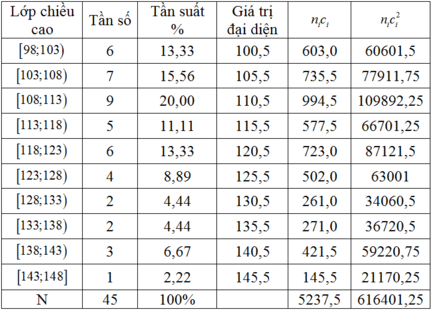
Phương sai của bảng số liệu.
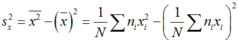
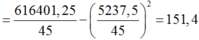

Để tính số trung vị, trước hết ta cần sắp xếp 45 số liệu đã cho theo thứ tự tăng dần. Số trung vị là giá trị của số liệu đứng thức N + 1 2 = 45 + 1 2 = 23 . Số liệu đứng thứ 23 là 123. Vậy số trung vị là 123.

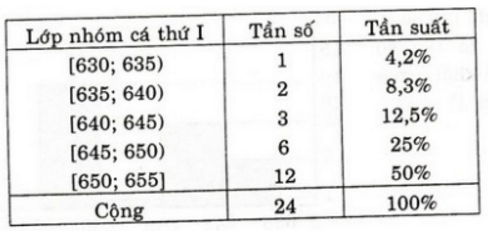
a) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
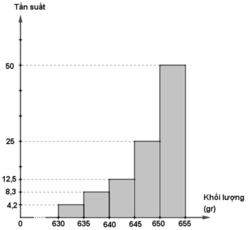
| [630;635) | 1 | 4,2% |
| [635;640) | 2 | 8,3% |
| [640;645) | 3 | 12,5% |
| [645;650) | 6 | 25% |
| [650;655] | 12 | 50% |
| Cộng | 24 | 100% |
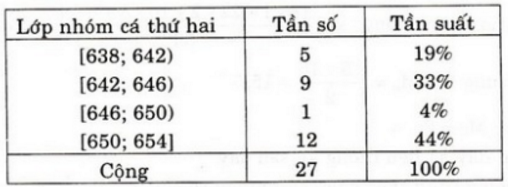
b) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
| [638;642) | 5 | 18,52% |
| [642;646) | 9 | 33,33% |
| [646;650) | 1 | 3,7% |
| [650;654) | 12 | 44,45% |
| Cộng | 27 | 100% |
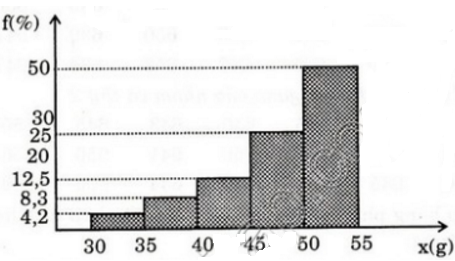
c) Biểu đồ tần suất hình cột:
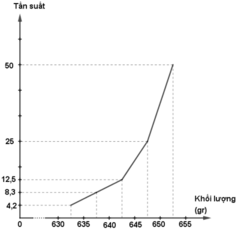
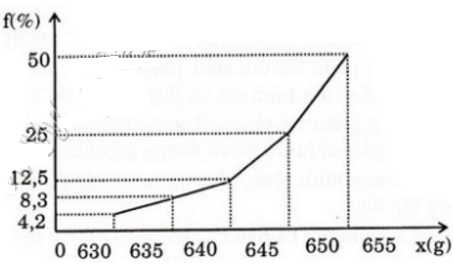
- Đường gấp khúc tần suất
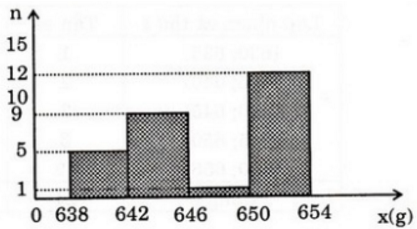
d) Biểu đồ tần số
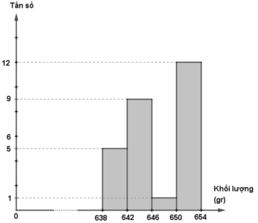
- Đường gấp khúc tần số
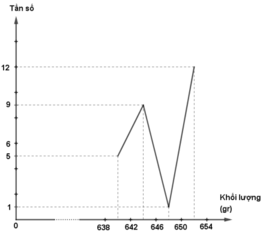
e) * Xét bảng phân bố ở câu a)
- Số trung bình:
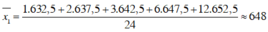
- Phương sai:
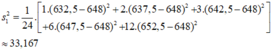
- Độ lệch chuẩn:
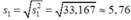
* Xét bảng phân bố ở câu b):
- Số trung bình:
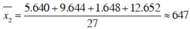
- Phương sai:
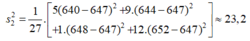
- Độ lệch chuẩn:
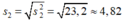
Nhận thấy s2 < s1 nên nhóm cá thứ hai có khối lượng đồng đều hơn.

Chọn A.
Lập bảng phân bố tần số; tần suất
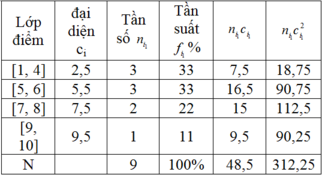
Điểm trung bình cộng của nhóm là:
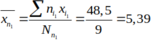

Chọn A.
Từ bảng số liệu đã cho ta có bảng phân bố tần số; tần suất ghép lớn như sau:
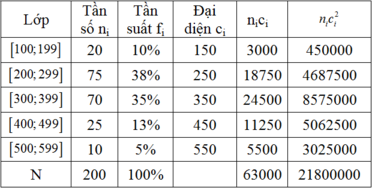
Dựa vào bảng trên ta có số trung bình cộng của dãy số liệu là:

a) Bảng phân bố tần số và tần suất:
b) Bảng phân bố tần số và tần suất:
c) Biểu đồ tần suất hình cột:
- Đường gấp khúc tần suất
d) Biểu đồ tần số
- Đường gấp khúc tần số
e) Xét bảng phân bố ở câu a)
- Số trung bình cộng:
Từ đó ta thấy nhóm cá thứ 2 có khối lượng đồng đều hơn.

a) Bảng phân bố tần số và tần suất ghép lớp:
| Lớp | Tần số | Tần suất |
|---|---|---|
| [6,5; 7,0) | 2 | 5,7% |
| [7,0; 7,5) | 4 | 11,5% |
| [7,5; 8,0) | 9 | 25,7% |
| [8,0; 8,5) | 11 | 31,4% |
| [8,5; 9,0) | 6 | 17,1% |
| [9,0; 9,5] | 3 | 8,6% |
| Cộng | 35 | 100% |
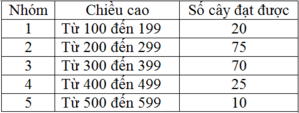
b) Nhận xét:
- Cây bạch đàn có chiều cao từ 7,0 m đến gần 8,5 m chiếm tỉ lệ chủ yếu.
- Các cây bạch đàn cao từ 6,5 m đến gần 7,0 m hoặc cao từ 9,0 m đến 9,5 m chiếm tỉ lệ rất ít.

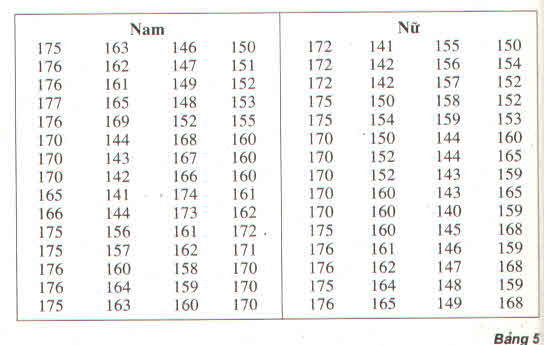
a) Tính chiều cao trung bình của học sinh nam
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp :
\(\overline{x}=\dfrac{1}{60}\left(5.140+9.150+19.160+17.170+10.180\right)\)
\(\overline{x}=163\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(8,33.140+15.150+31,67.160+28,33.170+16,67.180\right)\)\(\overline{x}=163\)
Tính chiều cao trung bình của học sinh nữ:
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp \(\overline{x}=\dfrac{1}{60}\left(8.140+15.150+16.160+14.170+7.180\right)\)
\(\overline{x}=159,5\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(13,33.140+25.150+26,67.160+23,33.170+11,67.180\right)\)
\(\overline{x}=159,5\)
b) Vì \(\overline{x}_{nam}=163>\overline{x}_{nữ}=159,5\) nên suy ra học sinh ở nhóm nam cao hơn học sinh ở nhóm nữ
c) \(\overline{x}=\left(60.159,5+60.163\right)\dfrac{1}{2}\approx161\left(cm\right)\)
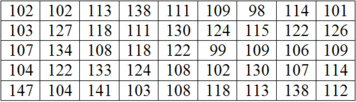

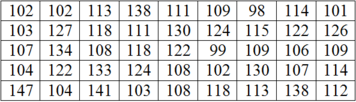
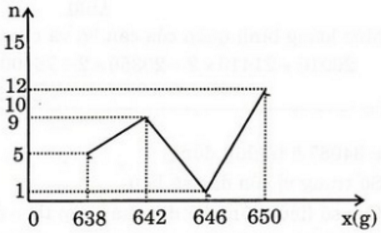


Chọn B
Dựa vào bảng phân dữ liệu đề bài cho ta có bảng phân bố tần số, tần suất như sau:
Số trung bình cộng của bảng số liệu: