
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\overrightarrow{AB}=\left(1;-2\right)\Rightarrow AB=\sqrt{1^2+\left(-2\right)^2}=\sqrt{5}\)
(C) tâm A đi qua B nên có bán kính \(R=AB=\sqrt{5}\)
Phương trình:
\(\left(x-1\right)^2+\left(y-1\right)^2=5\)

- Với \(m=1\) BPT trở thành \(2>0\) (thỏa mãn) (1)
- Với \(m\ne1\) tập nghiệm của BPT là R khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1>0\\\Delta'=\left(m-1\right)^2-2\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left(m-1\right)\left(m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\1< m< 3\end{matrix}\right.\)
\(\Leftrightarrow1< m< 3\) (2)
Kết hợp (1) và (2): với \(1\le m< 3\) thì BPT có tập nghiệm R

c.
\(\Leftrightarrow\left\{{}\begin{matrix}2x+1>0\\\left(2x+1\right)^2>\left(x+2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>-\dfrac{1}{2}\\x^2>1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>-\dfrac{1}{2}\\\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x>1\)
d.
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\2-x< 0\end{matrix}\right.\\\left\{{}\begin{matrix}2-x\ge0\\x>\left(2-x\right)^2\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x>2\end{matrix}\right.\\\left\{{}\begin{matrix}x\le2\\x^2-5x+4< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x>2\\\left\{{}\begin{matrix}x\le2\\1< x< 4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x>2\\1< x\le2\end{matrix}\right.\)
\(\Leftrightarrow x>1\)
2.
Do \(a\in\left(\dfrac{\pi}{2};\pi\right)\Rightarrow sina>0\)
\(\Rightarrow sina=\sqrt{1-cos^2a}=\sqrt{1-\left(-\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)


3.
Do \(sin\left(x+k2\pi\right)=sinx\Rightarrow sin\left(x+2020\pi\right)=sinx\)
\(sin\left(\dfrac{\pi}{2}+x\right)=cos\left(\dfrac{\pi}{2}-\dfrac{\pi}{2}-x\right)=cos\left(-x\right)=cosx\)
\(A=\dfrac{sinx+sin3x+sin5x}{cosx+cos3x+cos5x}=\dfrac{sinx+sin5x+sin3x}{cosx+cos5x+cos3x}\)
\(=\dfrac{2sin3x.cosx+sin3x}{2cos3x.cosx+cos3x}=\dfrac{sin3x\left(2cosx+1\right)}{cos3x\left(2cosx+1\right)}\)
\(=\dfrac{sin3x}{cos3x}=tan3x\)
4.
a.
\(\overrightarrow{CB}=\left(2;-2\right)=2\left(1;-1\right)\)
Do đường thẳng d vuông góc BC nên nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình đường thẳng d đi qua \(A\left(-1;2\right)\) và có 1 vtpt là \(\left(1;-1\right)\) là:
\(1\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow x-y+3=0\)
b.
Gọi \(I\left(a;b\right)\) là tâm đường tròn, ta có \(\left\{{}\begin{matrix}\overrightarrow{AI}=\left(a+1;b-2\right)\\\overrightarrow{BI}=\left(a-3;b-2\right)\\\overrightarrow{CI}=\left(a-1;b-4\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AI^2=\left(a+1\right)^2+\left(b-2\right)^2\\BI^2=\left(a-3\right)^2+\left(b-2\right)^2\\CI^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
Do I là tâm đường tròn qua 3 điểm nên: \(\left\{{}\begin{matrix}AI=BI\\AI=CI\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}AI^2=BI^2\\AI^2=CI^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a+1\right)^2+\left(b-2\right)^2=\left(a-3\right)^2+\left(b-2\right)^2\\\left(a+1\right)^2+\left(b-2\right)^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8a=8\\4a+4b=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\) \(\Rightarrow I\left(1;2\right)\)
\(\overrightarrow{AI}=\left(2;0\right)\Rightarrow R=AI=\sqrt{2^2+0^2}=2\)
Pt đường tròn có dạng:
\(\left(x-1\right)^2+\left(y-2\right)^2=4\)

2.
Xét BPT: \(\left(x+3\right)\left(4-x\right)>0\Leftrightarrow-3< x< 4\) \(\Rightarrow D_1=\left(-3;4\right)\)
Xét BPT: \(x< m-1\) \(\Rightarrow D_2=\left(m-1;+\infty\right)\)
Hệ có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)
\(\Leftrightarrow m-1< 4\)
\(\Leftrightarrow m< 5\)
3.
\(\dfrac{\pi}{24}=\dfrac{180^0}{24}=7^030'\)
4.
\(x^2+y^2-x+y+4=0\) không phải đường tròn
Do \(\left(\dfrac{1}{2}\right)^2+\left(-\dfrac{1}{2}\right)^2-4< 0\)
5.
\(f\left(x\right)=ax^2+bx+c\) có \(\left\{{}\begin{matrix}a\ne0\\\Delta=b^2-4ac< 0\end{matrix}\right.\) thì \(f\left(x\right)\) không đổi dấu trên R
6.
\(sin2020a=sin\left(2.1010a\right)=2sin1010a.cos1010a\)
7.
Công thức B sai
\(cos^2a+sin^2a=1\) , không phải \(cos2a\)

Câu 17: Ý A
\(\Delta:2x+3y-2=0\)
Kẻ đt d vuông góc với \(\Delta\) và đi qua M => Đường thẳng d có dạng: \(d:-3x+2y+c=0\)
\(M\in\left(d\right)\Rightarrow-3.3+2.3+c=0\Leftrightarrow c=3\)
\(\Rightarrow d:-3x+2y+3=0\)
Tọa độ hình chiếu vuông góc của M lên đt \(\Delta\) là nghiệm của hệ: \(\left\{{}\begin{matrix}2x+3y-2=0\\-3x+2y+3=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
Câu 18: B
Hàm có TXĐ là R khi \(x^2-2mx-2m+3\ge0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\left(lđ\right)\\\Delta\le0\end{matrix}\right.\)\(\Rightarrow4m^2-4\left(-2m+3\right)\le0\)\(\Leftrightarrow-3\le m\le1\)
Có 5 giá trị nguyên của m
Câu 19: A
Bpt vô nghiệm khi \(x^2-mx+1>0;\forall x\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow m^2-4< 0\Leftrightarrow-2< m< 2\)
Câu 20: D
\(D\in\Delta\Rightarrow D\left(t;-3t-2\right)\)
\(\Rightarrow\overrightarrow{AD}\left(t+1;-3t-2\right)\)
\(\overrightarrow{BC}\left(2;-1\right)\)
Vì ABCD là hình thang có một đáy là AD
\(\Rightarrow\)\(AD//BC\)
\(\Rightarrow\overrightarrow{AD}\) và \(\overrightarrow{BC}\) cùng phương
\(\Leftrightarrow\left(t+1\right)\left(-1\right)=2\left(-3t-2\right)\)\(\Leftrightarrow t=-\dfrac{3}{5}\)\(\Rightarrow D\left(-\dfrac{3}{5};\dfrac{-1}{5}\right)\)


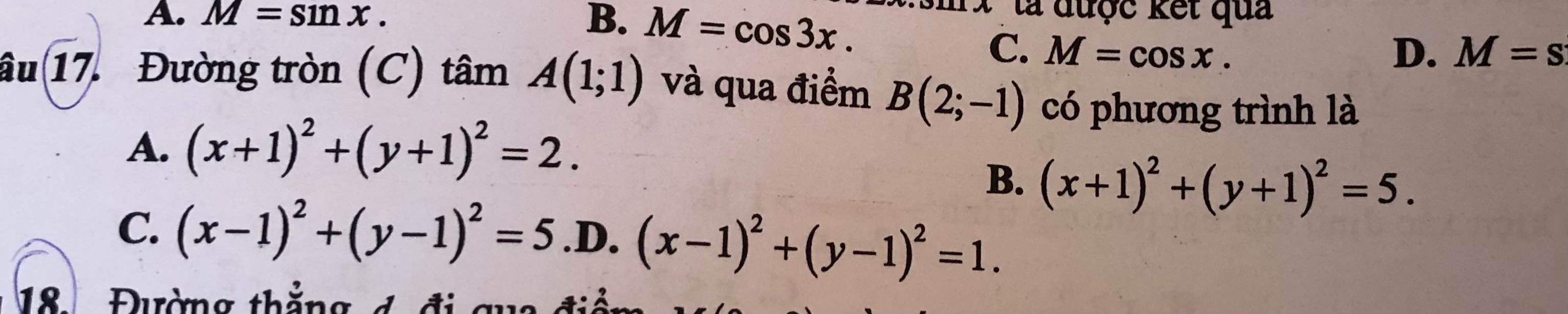








Xét ΔMNP có MJ là đường trung tuyến và G là trọng tâm
nên M,G,J thẳng hàng và \(MG=\dfrac{2}{3}MJ\)
Xét ΔMNP có MJ là đường trung tuyến
nên \(\overrightarrow{MJ}=\dfrac{1}{2}\left(\overrightarrow{MN}+\overrightarrow{MP}\right)\)
=>\(\overrightarrow{MG}=\dfrac{2}{3}\cdot\dfrac{1}{2}\left(\overrightarrow{MN}+\overrightarrow{MP}\right)=\dfrac{1}{3}\overrightarrow{MN}+\dfrac{1}{3}\overrightarrow{MP}\)
=>Chọn C