Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mẫu 1 có độ pH là:
\(pH=-log\left[H^+\right]=-log\left(8\cdot10^{-7}\right)=-log8+7=-3log2+7\)
Mẫu 2 có độ pH là:
\(pH'=-log\left[H^+\right]=-log\left(2\cdot10^{-9}\right)=-log2+9\)
Ta có:
\(pH-pH'=-3log2+7+log2-9=-2log2-2< 0\\ \Rightarrow pH< pH'\)
Mẫu 2 có độ pH lớn hơn mẫu 1.

\(pH=-log\left[H^+\right]=-log\left[10^{-4}\right]=4\)
\(pH=-log\left[H^+\right]=-log\left[10^{-5}\right]=5\)

tham khảo
Ta có:
\(pH=-logx\Leftrightarrow6,5=-logx\Leftrightarrow logx=-6,5\Leftrightarrow x=10^{-6,5}\approx3,16.10^{-77}\)
Vậy nồng độ \(H^+\) của sữa bằng \(3,16.10^{-7}\) mol/L.

Với \(pH=-log\left[H^+\right]\),ta có:
\(\dfrac{dpH}{d\left[H^+\right]}=\dfrac{d}{d\left[H^+\right]}\left(-log\left[H^+\right]\right)\)
Sử dụng quy tắc tính đạo hàm của hàm hợp, ta có:
\(\dfrac{dpH}{d\left[H^+\right]}=-1.\dfrac{d}{d\left[H^+\right]}\left(log\left[H^+\right]\right)\)
Áp dụng công thức đạo hàm của hàm số logarit tổng quát, ta có:
\(\dfrac{dpH}{d\left[H^+\right]}=-1.\dfrac{1}{\left[H^+\right]ln10}\)
Vậy tốc độ thay đổi của \(pH\) đối với nồng độ \(\left[H^+\right]\) là:
\(\dfrac{dpH}{d\left[H^+\right]}=-\dfrac{1}{\left[H^+\right]ln10}\)

\(a,pH_A=1,9\Leftrightarrow-log\left[H^+\right]=1,9\Leftrightarrow H^+=10^{-1,9}\)
Vậy độ acid của dung dịch A là \(10^{-1,9}mol/L\)
\(pH_B=2,5\Leftrightarrow-log\left[H^+\right]=2,5\Leftrightarrow H^+=10^{-2,5}\)
Vậy độ acid của dung dịch B là \(10^{-2,5}mol/L\)
Ta có: \(\dfrac{H^+_A}{H_B^+}=\dfrac{10^{-1,9}}{10^{-2,5}}\approx398\)
Vậy độ acid của dung dịch A cao hơn độ acid của dung dịch B 3,98 lần.
b, Ta có:
\(6,5< pH< 6,7\\ \Leftrightarrow6,5< -log\left[H^+\right]< 6,7\\ \Leftrightarrow-6,7< log\left[H^+\right]< -6,5\\ \Leftrightarrow10^{-6,7}< H^+< 10^{-6,5}\)
Vậy nước chảy từ vòi nước có độ acid từ \(10^{-6,7}mol/L\) đến \(10^{-6,5}mol/L\)
Như vậy, nước đó có độ acid cao hơn nước cất.

a)Độ pH của nước cất là:
\(pH=-log\left[H^+\right]=-log\left[10^{-7}\right]=7\)
b)Độ pH của dung dịch đó là:
\(pH=-log\left[H^+\right]=-log\left[20.10^{-7}\right]\approx5,7\)

pH=-log[H+]
Nồng độ ion hydro khi pH=8 là \(\left[H^+\right]=10^8\)(mol/lít)

a) Phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu là:
\(S=2S.e^{1,14.t}\Leftrightarrow2e^{1,14t}=1\Leftrightarrow e^{1,14t}=\dfrac{1}{2}\)
b) Phương trình vừa tìm được có ẩn là t và nằm ở vị trí mũ của lũy thừa

Tham khảo:
a) Hai vị trí \(O\) và \(A\) là hai vị trí chân cầu, tại hai vị trí này ta có: \(y = 0\)
\( \Leftrightarrow 4,8 \cdot \sin \frac{x}{9} = 0 \Leftrightarrow \sin \frac{x}{9} = 0 \Leftrightarrow \frac{x}{9} = k\pi (k \in \mathbb{Z}) \Leftrightarrow x = 9k\pi (k \in \mathbb{Z})\)
Quan sát đồ thị ta thấy, đồ thị hàm số \({\rm{y}} = 4,8 \cdot \sin \frac{x}{9}\) cắt trục hoành tại điểm 0 và \({\rm{A}}\) liên tiếp nhau với \(x \ge 0\).
Xét \({\rm{k}} = 0\), ta có \({{\rm{x}}_1} = 0\);
Xét \({\rm{k}} = 1\), ta có \({{\rm{x}}_2} = 9\pi \).
Mà \({x_1} = 0\) nên đây là hoành độ của 0 , do đó \({x_2} = 9\pi \) là hoành độ của điểm \(A\).
Khi đó \(OA = 9\pi \approx 28,3\).
Vậy chiều rộng của con sông xấp xỉ 28,3 m.
b) Do sà lan có độ cao 3,6 m so với mực nước sông nên khi sà lan đi qua gầm cầu thì ứng với \({\rm{y}} = 3,6\).
\( \Leftrightarrow 4,8 \cdot \sin \frac{x}{9} = 3,6 \Leftrightarrow \sin \frac{x}{9} = \frac{3}{4} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\frac{{\rm{x}}}{9} \approx 0,848 + {\rm{k}}2\pi }\\{\frac{{\rm{x}}}{9} \approx \pi - 0,848 + {\rm{k}}2\pi }\end{array}} \right.\)
(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp \(SHIFT\)\sin 3 \div 4 = ta được kết quả gần đúng là 0,85) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{\rm{x}} \approx 7,632 + 18{\rm{k}}\pi }\\{{\rm{x}} \approx 9\pi - 7,632 + 18{\rm{k}}\pi }\end{array}({\rm{k}} \in \mathbb{Z})} \right.\)
Xét \({\rm{k}} = 0\), ta có \({{\rm{x}}_1} \approx 7,632;{{\rm{x}}_2} \approx 20,642\).
Ta biểu diễn các giá trị \(x\) vừa tìm được trên hệ trục tọa độ vẽ đồ thị hàm số \(y = \) 4,8. \(\sin \frac{x}{9}\) như sau:
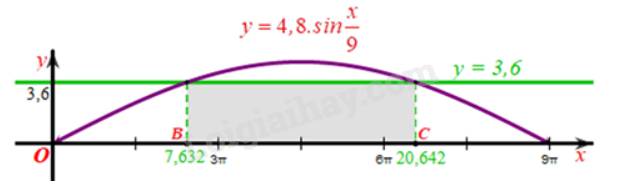
Khi đó để sà lan có thể đi qua được gầm cầu thì khối hàng hóa có độ cao 3,6 m phải có chiều rộng nhỏ hơn độ dài đoạn thẳng \({\rm{BC}}\) trên hình vẽ.
Mà \(BC \approx 20,642 - 7,632 = 13,01(m) < 13,1(m)\).
Vậy chiều rộng của khối hàng hoá đó phải nhỏ hơn 13,1 m.
c) Giả sử sà lan chở khối hàng được mô tả bởi hình chữ nhật MNPQ:
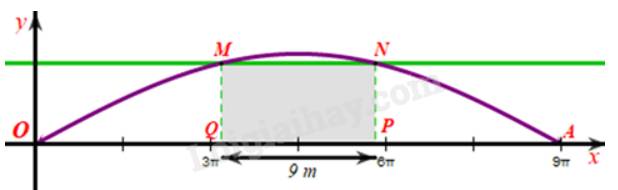
Khi đó \(QP = 9;OA = 28,3\) và \(OQ = PA\).
Mà \(OQ + QP + PA = OA \Rightarrow OQ + 9 + OQ \approx 28,3 \Rightarrow OQ \approx 9,65\)
Khi đó \({y_M} = 4,8 \cdot \sin \frac{{{x_M}}}{9} = 4,8 \cdot \sin \frac{{OQ}}{9} \approx 4,8 \cdot \sin \frac{{9,65}}{9} \approx 4,22(\;{\rm{m}}) < 4,3\) (m).
Vậy để sà lan có thể đi qua được gầm cầu thì chiều cao của khối hàng hoá đó phải nhỏ hơn 4,3 m.
a) Ta có:\(-\log\left[H^+\right]=6.1\Leftrightarrow-\log x=6,1\)
b) Phương trình vừa tìm được có ẩn là x và nằm ở vị trí hệ số của logarit