Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Gọi M 1 , M 2 , M lần lượt là điểm biểu diễn của các số phức z 1 , 2 z 2 , z trên mặt phẳng tọa độ Oxy.
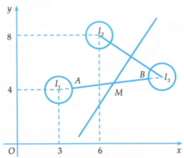
Do z 1 - 3 - 4 i = 1 nên quỹ tích điểm M 1 là đường tròn C 1 có tâm I 1 3 ; 4 và bán kính R = 1
Do z 2 - 3 - 4 i = 1 2 ⇔ 2 z 2 - 6 - 8 i = 1 nên quỹ tích điểm M 2 là đường tròn C 2 có tâm I 2 6 ; 8 và bán kính R = 2
Ta có điểm M(a; b) thỏa mãn 3a - 2b = 12 nên quỹ tích điểm M là đường thẳng d: 3x - 2y - 12 = 0
Khi đó
![]()
Gọi C 3 là đường tròn đối xứng với đường tròn C 2 qua đường thẳng d.
Ta tìm được tâm của C 3 là I 3 138 13 ; 64 13 và bán kính R = 1
Khi đó
![]()
với M 3 ∈ C 3 và A, B lần lượt là giao điểm của đường thẳng I 1 I 3 với hai đường tròn C 1 , C 3 (quan sát hình vẽ).
Dấu "=" xảy ra khi và chỉ khi M 1 ≡ A và M 3 ≡ B
Vậy P m i n = A B + 2 = I 1 I 3 = 3 1105 13

Đáp án B
Phương pháp:
+) Tìm điều kiện để phương trình y’ = 0 có hai nghiệm phân biệt thỏa mãn ĐKXĐ.
+) Viết phương trình đường thẳng AB. Để A, B, C thẳng hàng ó C ∈ AB
Cách giải: TXĐ: D = R\{|m|}
Ta có:
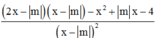
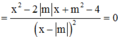
![]()
<=> 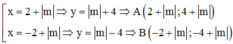
=> Đồ thị hàm số luôn có hai điểm cực trị A, B phân biệt.
Đường thẳng AB có phương trình:
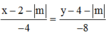
![]()
![]()
Để A, B, C(4;2) phân biệt thẳng hàng ó CAB => 2 = 4.2 - |m| ó |m| = 6
Khi đó ta có: B(4;2) ≡ C => không thỏa mãn.
Vậy không có giá trị nào của m thỏa mãn yêu cầu bài toán

Bài 1:
a: \(\Leftrightarrow x\cdot\dfrac{3}{4}=-1\)
hay x=-4/3
b: =>x=4/8+3/7=1/2+3/7=7/14+6/14=13/14
Bài 3:
BCNN(16;32;5)=160
UCLN(16;32;5)=1





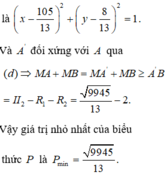
vì a/b=15/35=3/7
=>a:3=b:7
=>a=3/7b
mà ƯCLN(a,b).BCNN(a,b)=a.b
=>3/7b.b=3549
=>b=91, a=3/7b=39
Ta có: \(\frac{a}{b}\)= \(\frac{15}{35}\)= \(\frac{3}{7}\).
Suy ra: a= 3K; b= 7K, với k thuộc N*.
Ta có: ƯCLN (a,b)= ƯCLN(3K,7K)= K