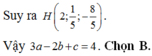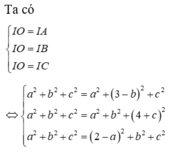Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Từ đề bài ta có \(A\left(n;0;0\right);B\left(0;m;0\right);C\left(0;0;1\right)\)
Gọi \(r\) là bán kính đường tròn ngoại tiếp tam giác vuông \(OAB\)
\(\Rightarrow r=\frac{AB}{2}=\frac{1}{2}\sqrt{m^2+n^2}\)
\(\Rightarrow R=\sqrt{\left(\frac{OC}{2}\right)^2+r^2}=\sqrt{\frac{1}{4}+\frac{1}{4}\left(m^2+n^2\right)}=\frac{1}{2}\sqrt{m^2+n^2+1}\)
Do \(m+2n=1\Rightarrow m=1-2n\)
\(\Rightarrow R=\frac{1}{2}\sqrt{\left(1-2n\right)^2+n^2+1}=\frac{1}{2}\sqrt{5n^2-4n+2}\)
\(\Rightarrow R=\frac{1}{2}\sqrt{5\left(n-\frac{2}{5}\right)^2+\frac{6}{5}}\ge\frac{1}{2}\sqrt{\frac{6}{5}}\)
\(\Rightarrow R_{min}=\frac{1}{2}\sqrt{\frac{6}{5}}=\frac{\sqrt{30}}{10}\) khi \(n=\frac{2}{5}\Rightarrow m=\frac{1}{5}\Rightarrow2m+n=\frac{4}{5}\)
Đáp án A
Phương pháp giải: Xác định tọa độ ba điểm A, B, C và gọi tâm I, sử dụng điều kiện cách đều IA=IB=IC=IO để tìm tọa độ tâm I của mặt cầu
Lời giải:
Gọi A(a;0;0), B(0;b;0), C(0;0;c) => Tọa độ trọng tâm G là
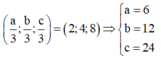
Gọi tâm mặt cầu (S) là I(x;y;z) => IO =IA = IB =IC
Vậy tọa độ tâm mặt cầu là I(3;6;12)
Chọn A
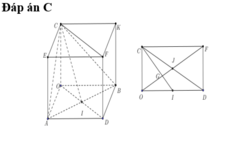
Gọi I (a;b;c)
Ta có IA=IO=R ó hình chiếu của I lên OA là trung điểm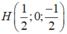 
của OA.
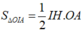
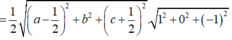
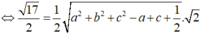
Theo bài ra ta có:
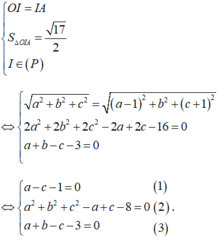
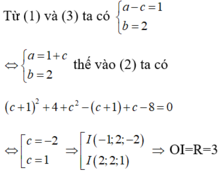
Đáp án D.
Mặt cầu tiếp xúc với cả ba mặt cầu trên là mặt cầu tiếp xúc ngoài với cả 3 mặt cầu trên. Gọi I là tâm và R là bán kính mặt cầu cần tìm
Ta có:
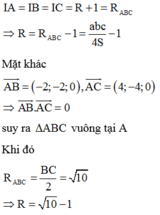
Chọn A
Điểm M(1;0;0) là 1 điểm thuộc (P)
Vì (P) // (Q) nên
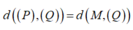
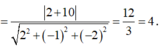
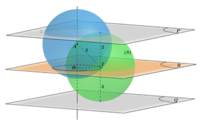
Giả sử I(a;b;c) là tâm của (S). Vì (S) tiếp xúc với cả (P) và (Q) nên bán kính mặt cầu (S) là:
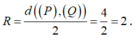
Do đó IA = 2 nên I luôn thuộc mặt cầu (T) tâm A, bán kính 2.
Ngoài ra
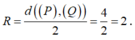
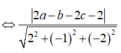
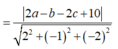
Do đó I luôn thuộc mặt phẳng (R): 2x-y-2z+4=0.
Gọi H là hình chiếu vuông góc của A lên (R). Vì A, (R) cố định nên H cố định.
Ta có
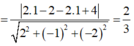
do đó tam giác AHI vuông tại H nên
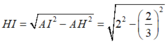
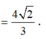
Vậy I luôn thuộc đường tròn tâm H, nằm trên mặt phẳng (R), bán kính
