Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
, 
và 
;
, 
và 
;
Tham khảo:
a)
b) Cỡ mẫu \(n = 60\)
Tứ phân vị thứ nhất \({Q_1}\) là \(\frac{{{x_{15}} + {x_{16}}}}{2}\). Do \({x_{15}},\;{x_{16}}\) đều thuộc nhóm \(\left[ {40;50} \right)\) nên nhóm náy chứa \({Q_1}\). Do đó,
\(p = 5;\;\;{a_5} = 40;\;\;{m_5} = 15;\;\;{m_1} + {m_2} + {m_3} + {m_4} = 1 + 2 + 4 + 6 = 13;\;{a_6} - {a_5} = 10\)
Ta có \({Q_1} = 40 + \frac{{\frac{{60}}{4} - 13}}{{15}} \times 10 = 41,33\)
Ý nghĩa: Có 25% số giá trị nhỏ hơn 41,33
Tứ phân vị thứ hai, \({M_e}\) là \(\frac{{{x_{30}} + {x_{31}}}}{2}\). Do \({x_{30}};\;{x_{31}}\) đều thuộc nhóm \(\left[ {50;60} \right)\) nên nhóm này chứa \({M_e}\). Do đó,
\(p = 6;\;\;{a_6} = 50;\;\;{m_6} = 12;\;\;{m_1} + {m_2} + {m_3} + {m_4} + {m_5} = 1 + 2 + 4 + 6 + 15 = 13;\;{a_7} - {a_6} = 10\)
Ta có: \({Q_2} = 50 + \frac{{\frac{{60}}{2} - 28}}{{12}} \times 10 = 51,66\)
Ý nghĩa: Có 50% số giá trị nhỏ hơn 51,66
Tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{45}} + {x_{46}}}}{2}\). Do \({x_{45}},\;{x_{46}}\) đều thuộc nhóm \(\left[ {60;70} \right)\) nên nhóm náy chứa \({Q_3}\). Do đó,
\(p = 7;\;\;{a_7} = 60;\;\;{m_7} = 10;\;\;{m_1} + {m_2} + {m_3} + {m_4} + {m_5} + {m_6} = 1 + 2 + 4 + 6 + 15 + 12 = 40; {a_8} - {a_7} = 10\).
Ta có: \({Q_3} = 60 + \frac{{\frac{{60 \times 3}}{4} - 40}}{{10}} \times 10 = 65\)
Ý nghĩa: Có 75% số giá trị nhỏ hơn 65.
a) \(100+98+96+...+2-97-95-93-...-3\)
= \(100+98+\left(96-97\right)+\left(94-95\right)+...+\left(2-3\right)\)
= \(100+98-95\) = \(103\)
b) \(2-4-6+8+10-12-14+16+...-102+104\)
= \(\left(2-4\right)+\left(-6+8\right)+\left(10-12\right)+\left(-14+16\right)+...+\left(-102+104\right)\)
= \(-2+2-2+2-2+...+2\) = \(0\)
c) \(1+2-3-4+5+6-7-8+9+10-11-12+...-111-112+113+114\)
= \(\left(1+2\right)-\left(3+4\right)+\left(5+6\right)-\left(7+8\right)+...\left(113+114\right)\)
= \(3-7+11-15+19-23+...+219-223+227\)
= \(\left(3-7\right)+\left(11-15\right)+\left(19-23\right)+...+\left(219-223\right)+227\)
= \(-4-4-4-4-...-4+227\)
= \(54\left(-4\right)+227\) = \(-216+227\) = \(11\)
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:
Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right) = \frac{1}{2}\left( {11 + 11} \right) = 11\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) = \frac{1}{2}\left( {14 + 14} \right) = 14\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right) = \frac{1}{2}\left( {21 + 22} \right) = 21,5\)
b)
c) Do số trận đấu là số nguyên nên ta hiệu chỉnh như sau:
Tổng trận đấu là: \(n = 4 + 8 + 2 + 6 = 20\).
Gọi \({x_1};{x_2};...;{x_{20}}\) là điểm số của các trận đấu được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_4} \in \begin{array}{*{20}{c}}{\left[ {5,5;10,5} \right)}\end{array};{x_5},...,{x_{12}} \in \begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array};{x_{13}},{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {15,5;20,5} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right)\)
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_{10}},{x_{11}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}.\left( {15,5 - 10,5} \right) = 14,25\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}.\left( {15,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 6;C = 4 + 8 + 2 = 14;{u_j} = 20,5;{u_{j + 1}} = 25,5\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}.\left( {25,5 - 20,5} \right) \approx 21,3\)
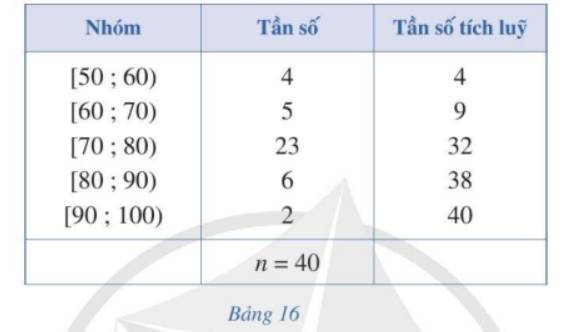
a,
Trung vị: \({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 70 + \left( {\frac{{20 - 9}}{{23}}} \right).10 = \frac{{1720}}{{23}} \approx 74,8\)
⇨ Chọn: B. 75
b,
- Tứ phân vị thứ hai \({Q_2} = {M_e} = 75\) => Loại A, C
- Tứ phân vị thứ nhất: \({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 70 + \left( {\frac{{10 - 9}}{{23}}} \right).10 = \frac{{1620}}{{23}} \approx 70\)
⇨ Chọn D
c,
\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 70 + \left( {\frac{{23 - 5}}{{2.23 - 5 - 6}}} \right).10 = \frac{{526}}{7} \approx 75\)
⇨ Chọn C
Tham khảo:
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:
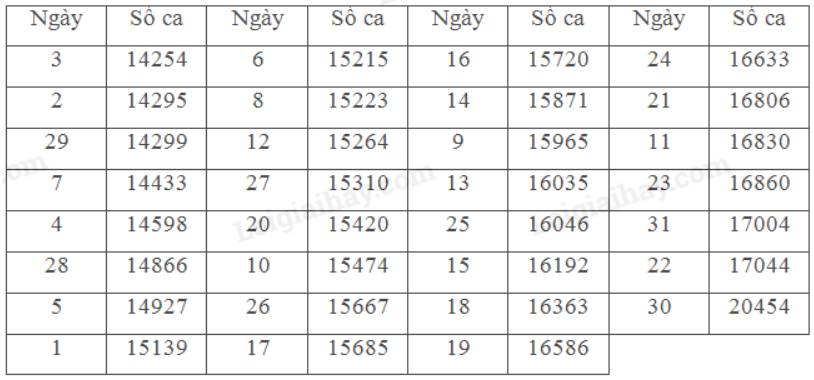
Số trung bình của số liệu là: \(\bar x \approx 15821,87\)
Tứ phân vị thứ nhất là: \({x_8} = 15139\)
Tứ phân vị thứ hai là: \({x_{16}} = 15685\)
Tứ phân vị thứ ba là: \({x_{24}} = 16586\)
Mẫu số liệu có 1 giá trị ngoại lệ.
b)
c) Ta có:
• Số ca nhiễm mới SARS-CoV-2 trung bình trong tháng 12/2021 tại Việt Nam là:
\(\bar x = \frac{{14.14,74 + 14.16,25 + 2.17,75 + 0.19,25 + 1.20,75}}{{31}} \approx 15,81\)
• Gọi \({x_1};{x_2};...;{x_{31}}\) số ca nhiễm mới SARS-CoV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_{14}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}}\end{array}}\end{array};{x_{15}},...,{x_{28}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}}\end{array};{x_{29}},{x_{30}} \in \begin{array}{*{20}{c}}{\left[ {17;18,5} \right)}\end{array};{x_{31}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {20;21,5} \right)}\end{array}}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \({x_{16}}\)
Ta có: \(n = 31;{n_m} = 14;C = 14;{u_m} = 15,5;{u_{m + 1}} = 17\)
Do \({x_{16}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 15,5 + \frac{{\frac{{31}}{2} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 15,66\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_8}\).
Ta có: \(n = 31;{n_m} = 14;C = 0;{u_m} = 14;{u_{m + 1}} = 15,5\)
Do \({x_8} \in \begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 14 + \frac{{\frac{{31}}{4} - 0}}{{14}}.\left( {15,5 - 14} \right) \approx 14,83\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{24}}\).
Ta có: \(n = 31;{n_j} = 14;C = 14;{u_j} = 15,5;{u_{j + 1}} = 17\)
Do \({x_{24}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 15,5 + \frac{{\frac{{3.31}}{4} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 16,49\)
