Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Vận tốc trung bình đi từ A đến B là:
$\frac{20+30}{2}=25$ (km/h)
Kiến thức cần nhớ:
Vận tốc trung bình bằng tổng quãng đường chia cho tổng thời gian đi hết quãng đường đó!
Công thức Vtb = \(\dfrac{S_1+S_2+...+S_n}{t_1+t_2+...+t_n}\)
Giải chi tiết:
Gọi quãng đường AB là: S (km); S > 0
Thời gian người đó đi hết nửa quãng đường đầu là:
\(\dfrac{S}{2}\) : 20 = \(\dfrac{S}{40}\) (giờ)
Thời gian người đó đi hết nửa quãng đường sau là:
\(\dfrac{S}{2}\) : 30 = \(\dfrac{S}{60}\) (giờ)
Vận tốc trung bình của người đó đi từ A đến B là:
Áp dụng công thức Vtb = \(\dfrac{S_1+S_2}{t_1+t_2}\) ta có
Vtb = \(\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{60}}\)
Vtb = \(\dfrac{S}{S.\left(\dfrac{1}{40}+\dfrac{1}{60}\right)}\)
Vtb = \(\dfrac{1}{\dfrac{1}{24}}\)
Vtb = 24 (km/h)

Gọi vận tốc trung bình của người đó là: x(km/h)
Gọi độ dài nửa quãng đường AB là: a(km)
Khi đó ta có:
+ Thời gian đi nửa quãng đường đầu là: a/20(h)
+ Thời gian đi nửa quãng đường sau là: a/30(h)
→ Thời gian đi cả quãng đường AB là:
Do đó ta có: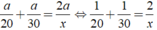
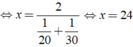
Vậy vận tốc cần tìm là 24km/h
Chọn đáp án B.

Gọi vận tốc trung bình của người đó là: x(km/h) (x > 0)
Gọi độ dài nửa quãng đường AB là: a(km)
Khi đó ta có:
+ Thời gian đi nửa quãng đường đầu là: a/20(h)
+ Thời gian đi nửa quãng đường sau là: a/30(h)
→ Thời gian đi cả quãng đường AB là:
Do đó ta có: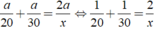
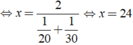
Vậy vận tốc cần tìm là 24km/h
Chọn đáp án B.

Vận tốc trung bình của người đó trên toàn bộ quãng đường AB là:
(15 + 30) : 2 = 22,5 (km/h)
Đáp số: 22,5 km/h

Bài giải
Vận tốc của người đó là :
( 1 + 1 ) : ( 1/20 + 1/30 ) = 28 ( km / giờ )
Đáp số : 28 km/h
Câu 1:
Áp dụng BĐT Cô si cho 4 số dương, ta có:
\(a^4+b^4+c^4+d^4\ge4.^4\sqrt{\left(abcd\right)^4}=4abcd\)
Dấu "=" \(\Leftrightarrow a=b=c=d\)
Câu 2:
Gọi quãng đường AB là x km (x>0)
\(V_{tb}=\dfrac{S}{t}=\dfrac{x}{\dfrac{x}{\dfrac{2}{20}}+\dfrac{x}{\dfrac{2}{30}}}=\dfrac{x}{\dfrac{x}{40}+\dfrac{x}{60}}=\dfrac{x}{\dfrac{5x}{120}}=\dfrac{120x}{5x}=\dfrac{120}{5}=24\left(\text{km/h}\right)\)
Vậy ...
cảm ơn ạ :D