Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Vì \((d_1)\parallel (d_2)\) \(\Rightarrow\left\{{}\begin{matrix}m-1=-2\\m-2\ne3\end{matrix}\right.\Rightarrow m=-1\)
2.a) (P) đi qua \(M\left(1;2\right)\Rightarrow2=a\Rightarrow y=2x^2\)
bạn tự vẽ nha
b) Gọi pt đường thẳng AB là \(y=ax+b\)
\(\Rightarrow\left\{{}\begin{matrix}3=2a+b\\0=-a+b\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3=2a+b\left(1\right)\\0=-2a+2b\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)+\left(2\right)\Rightarrow3b=3\Rightarrow b=1\Rightarrow a=1\Rightarrow y=x+1\)
pt hoành độ giao điểm \(2x^2-x-1=0\Rightarrow\left(x-1\right)\left(2x+1\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=2\\y=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\) tọa độ của 2 giao điểm là \(\left(1,2\right)\) và\(\left(-\dfrac{1}{2},\dfrac{1}{2}\right)\)

BÀI 1
để d1 và d2 // thì: m-3=-1(1) ; m khác 3 (2)
ta có: (1) <=> m=2 (3)
từ (2) và (3) => để d1//d2 thì m = 2

a: Tọa độ A là:
x-2=0 và y=3
=>x=2 và y=3
Tọa độ B là:
x+2=0và y=3
=>x=-2 và y=3
b: Tọa độ M là:
3-m(x-2)=3-m(x+2) và y=3-m(x-2)
=>-m(x-2)+m(x+2)=0 và y=3-m(x-2)
=>-mx+2m+mx+2m=0 và y=3-m(x-2)
=>m=0 và y=3
=>M(x;3)
c: để Mtrùng A thì x=2

a: tọa độ giao điểm M là:
\(\left\{{}\begin{matrix}2x-1=-x+2\\y=2x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)

Do (d1) song song với đường thẳng y = 2x nên a = 2
(d1): y = 2x + b
Thay tọa độ điểm (1; -1) vào (d) ta được:
2.1 + b = -1
⇔ b = -1 - 2
⇔ b = -3
Vậy (d1): y = 2x - 3
b) x = 0 ⇒ y = -3
*) Đồ thị:
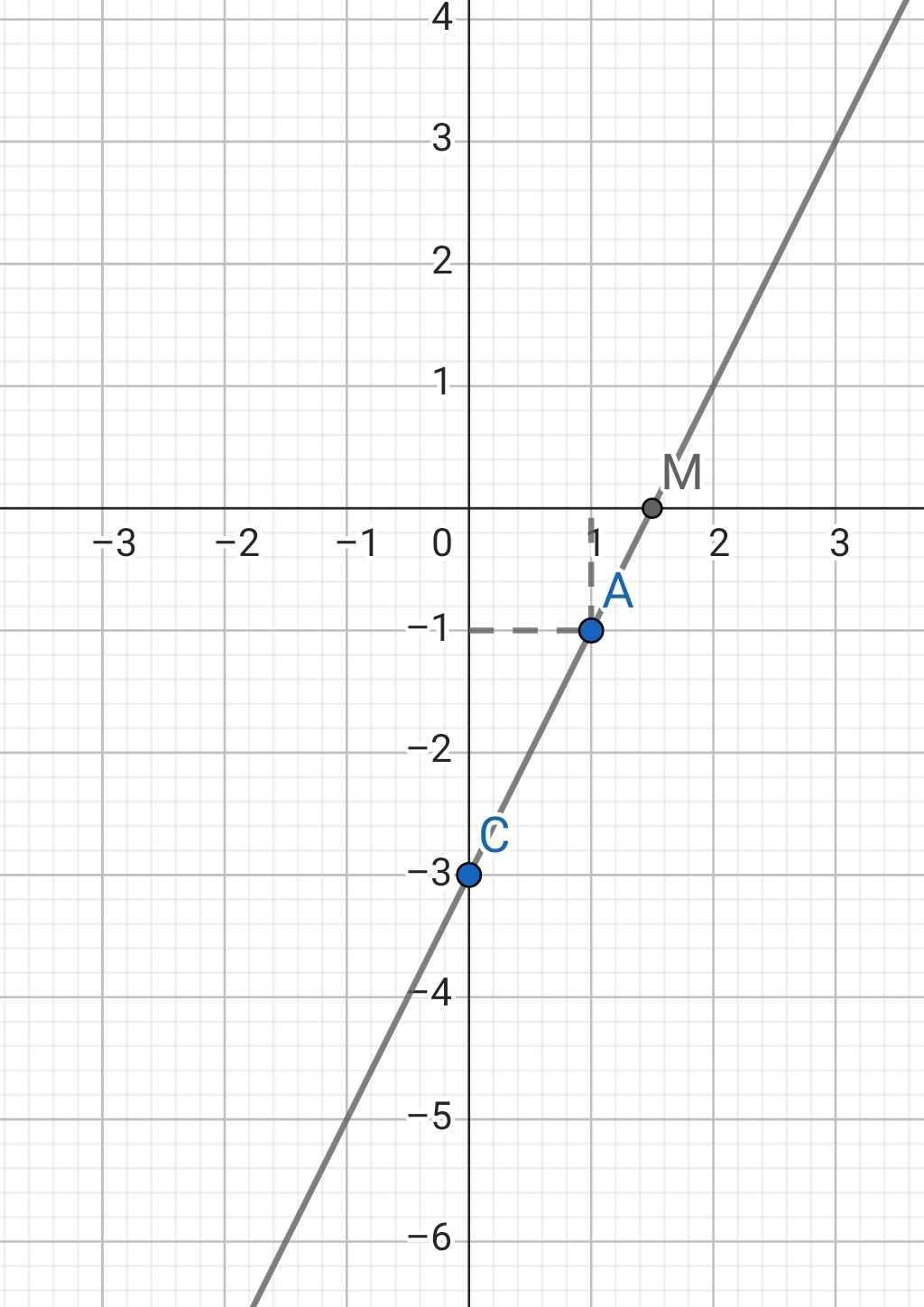
c) Phương trình hoành độ giao điểm của (d1) và (d2):
2x - 3 = 1/2 x + 1
⇔ 2x - 1/2 x = 1 + 3
⇔ 3/2 x = 4
⇔ x = 4 : 2/3
⇔ x = 8/3
⇒ y = 2.8/3 - 3 = 7/3
Vậy tọa độ giao điểm của (d1) và (d2) là (8/3; 7/3)
d) Ta có:
Gọi a là góc cần tính
⇒ tan(a) = 2
⇒ a ≈ 63⁰
(b) và (d) bạn tự xem kiến thức vẽ rồi áp dụng công thức tan là làm được nha=)
a)
Đồ thị hàm số (d1)// đường thẳng `y=2x`
=> \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b\ne0\end{matrix}\right.\)
=> `y=2x+b`
Do hàm số `y=2x+b` đi qua điểm `(1;-1)` nên `x=1`, `y=-1`:
`-1=2.1+b`
=> `b=-3`
Vậy hàm số `y=ax+b` là `y=2x-3`
c)
Ta có PTHĐGĐ giữa `d_1` và `d_2`:
\(2x-3=\dfrac{1}{2}x+1\\ \Rightarrow x=\dfrac{8}{3}\Rightarrow y=\dfrac{7}{3}\)
Vậy `E=`\(\left(\dfrac{8}{3};\dfrac{7}{3}\right)\)
$HaNa$

a) Tìm toạ độ giao điểm A của hai đường thẳng y = 3x - 2 (d1) và y = (2/3)x (d2):
Để tìm toạ độ giao điểm A của hai đường thẳng, ta có thể giải hệ phương trình sau:y = 3x - 2
y = (2/3)x
(2/3)x = 3x - 2
Giải phương trình này, ta được x = 3/4.Thay x = 3/4 vào phương trình y = (2/3)x, ta được y = (2/3)(3/4) = 7/4.Vậy toạ độ giao điểm A của hai đường thẳng (d1) và (d2) là A(3/4, 7/4).b) Viết phương trình đường thẳng (d) đi qua A và song song với đường thẳng (d3) là y = 3x - 1:
Để viết phương trình đường thẳng (d) đi qua A và song song với đường thẳng (d3), ta có thể sử dụng công thức sau:y - y0 = m(x - x0)
Trong đó, (x0, y0) là toạ độ của điểm A và m là hệ số góc của đường thẳng (d3).
Thay các giá trị này vào công thức trên, ta được:y - 7/4 = 3(x - 3/4)
Sau khi sắp xếp lại các số hạng, ta được phương trình đường thẳng (d) là: y = 3x - 5/4.
Câu 1 :
Để (d1) // (d2) :
m - 1 = -2
=> m = -1
bạn ơi cho mình hỏi: làm sao để có GP vậy ạ, và GP là gì ạ