VD
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
26 tháng 7 2019
Chọn A
Đồ thị của hàm số 
liên tục trên các đoạn 
và 
, lại có 
là một nguyên hàm của 
.
Do đó diện tích của hình phẳng giới hạn bởi các đường:
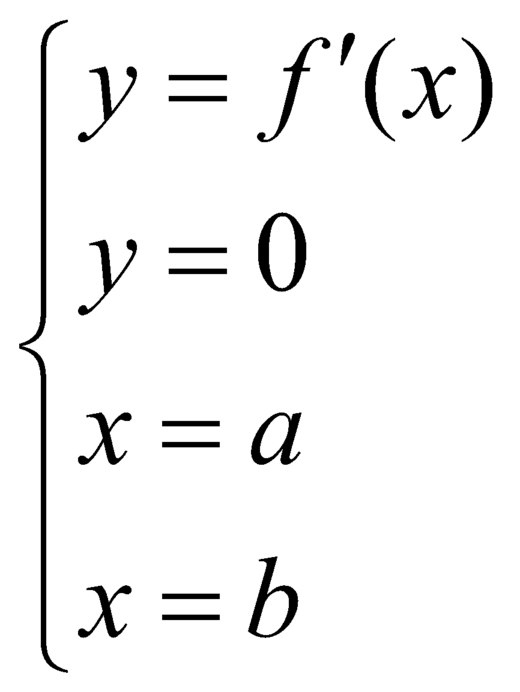là:
.
Vì 
Tương tự: diện tích của hình phẳng
giới hạn bởi các đường: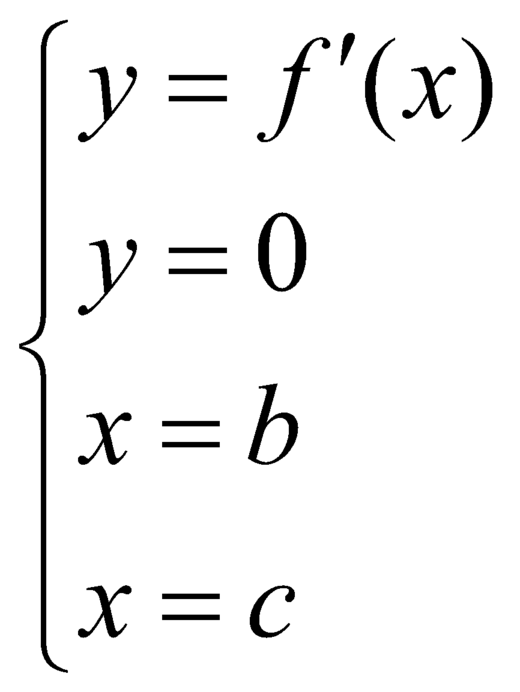 
là:
.
.
Mặt khác, dựa vào hình vẽ ta có: 
.
Từ (1), (2) và (3) ta chọn đáp án A.
( có thể so sánh 
với 
dựa vào dấu của 
trên đoạn 
và so sánh 
với 
dựa vào dấu của 
trên đoạn 
)
14 tháng 3 2021
a) f' (x)=3x2-6x
f'' (x)=6x-6;f'' (x)=0 < ⇒ x=1 ⇒ f (1) = -1
Vậy I(1; -1)
b) Công thức chuyển hệ trục tọa độ trong phép tịnh tiến theo vectơ OI:
Phương trình của (C) đối với hệ trục IXY là:
y - 1 = (X+1)3-3(X+1)2+1 hay Y=X3-3X
Vì hàm số Y=X3-3X là hàm số lẻ nên đồ thị của nó nhận gốc tọa độ I làm tâm đối xứng.
c) * Tiếp tuyến với (C) tại I(1; -1) đối với hệ tọa độ Oxy là:
y = f' (1)(x-1)+f(1) với f’(1) = -3; f(1) = -1
Nên Phương trình tiếp tuyến: y= -3(x-1)+(-1) hay y = -3x + 2
Xét hiệu (x3-3x2+1)-(-3x+2)=(x-1)3
Với x ∈(-∞;1) ⇒ (x-1)3<0 ⇔ x3 – 3x2 + 1 < -3x +2 nên đường cong (C): y=x3-33+1 nằm phía dưới tiếp tuyến y = -3x + 2
Với x ∈(1; +∞) ⇒ (x-1)3>0 ⇔ x3 – 3x2 + 1 > -3x + 2 nên đường cong (C): nằm phía trên tiếp tuyến tại I.
CM
17 tháng 3 2018
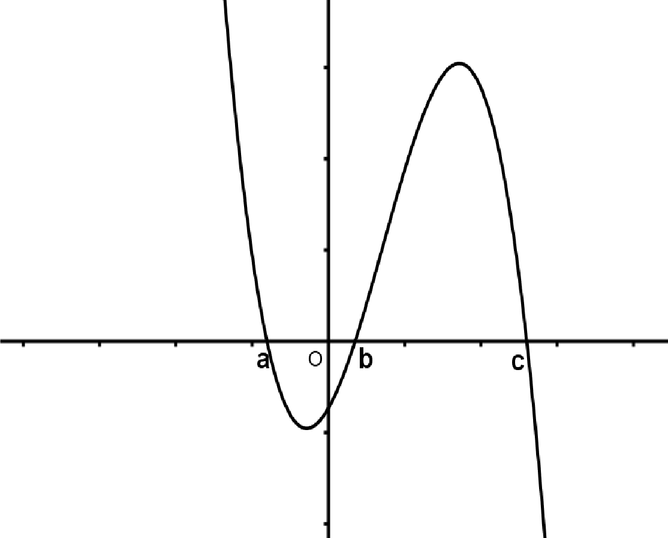
+Ta có đạo hàm f’ (x)= 3ax2+ 2bx+c .
+ Dựa vào đồ thị hàm số y= f’ ( x) ta thấy đồ thị hàm số đi qua các điểm (0 ; 0) ; (1 ; -1) ; (2 ; 0) nên a= 1/3 ; b= -1 ; c= 0.
Do vậy hàm số cần tìm có dạng y= 1/3 x3-x2+ d .
Điểm tiếp xúc với trục hoành là cực trị của đồ thị hàm số và tại đó ta có x= 0 hoặc x= 2. + Vì đồ thị hàm số y= f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương nên đồ thị hàm số tiếp xúc trục hoành tại điểm x= 2 nghĩa là:
f( 2) = 0 hay 8/3-4+ d= 0 nên d= 4/3
Chọn D.
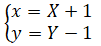
℃=℉ - 32/1.8000
℉ =℃ * 1.8000+ 32.00
1.8000 là 18000 nha đừng nhầm thành 1x18000