
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


e,\(3\frac{2}{7}x-\frac{1}{8}=2\frac{3}{4}\)
\(=>\frac{23}{7}x-\frac{1}{8}=\frac{11}{4}\)
\(=>\frac{23}{7}x=\frac{11}{4}+\frac{1}{8}=\frac{23}{8}\)
\(=>x=\frac{23}{8}:\frac{23}{7}\)
\(=>x=\frac{7}{8}\)

Bài 4
d. 450 : [ 41 - (2x - 5) ] = 32 . 5
450 : [ 41 - (2x - 5) ] = 9 . 5
450 : [ 41 - (2x - 5) ] = 45
[ 41 - (2x - 5) ] = 450 : 45
41 - (2x - 5) = 10
(2x - 5) = 41 - 10
2x - 5 = 31
2x = 31 + 5
2x = 36
x = 36 : 2
x = 1
e. 30 : (x - 7) = 1519 : 158
30 : (x - 7) = 15
x - 7 = 30 : 15
x - 7 = 2
x = 2 + 7
x = 9
f. (2x - 3)3 = 125
2x - 3 = 5
2x = 5 + 3
2x = 8
x = 8 : 2
x = 4
tk cho cj nha

b) \(5\frac{1}{4}.\frac{3}{8}+10\frac{3}{4}.\frac{3}{8}\)
\(=\left(5\frac{1}{4}+10\frac{3}{4}\right).\frac{3}{8}\)
\(=16.\frac{3}{8}=6\)
c) \(6\frac{1}{5}.\frac{-2}{7}+14\frac{4}{5}.\frac{-2}{7}\)
\(=\left(6\frac{1}{5}+14\frac{4}{5}\right).\frac{-2}{7}\)
\(=21.\frac{-2}{7}=-6\)

\(\Rightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{5}{4}+\dfrac{2}{5}=\dfrac{3}{10}x-\dfrac{1}{4}x\)
\(\Rightarrow\dfrac{33}{20}=\dfrac{11}{20}x\)
\(\Rightarrow x=\dfrac{33}{20}\div\dfrac{11}{20}\)
\(\Rightarrow x=3\)
\(1\dfrac{1}{4}-x\dfrac{1}{4}=x\cdot30\%\cdot\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-x\dfrac{1}{4}=x\cdot\dfrac{3}{10}-\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Leftrightarrow25-5x=6x-8\)
\(\Leftrightarrow-5x-6x=-8-25\)
\(\Leftrightarrow-11x=-33\)
\(\Leftrightarrow x=3\)
Vậy x = 3

a) Ư(60):{ 1;2;3;4;5;6;10;12;15;20;30;60}
Ư(84):{ 1;2;4;6;7;12;14;21;42;84}
Ư(120):{ 1;2;3;4;5;6;8;10;12;15;20;24;30;40;60;120}
ƯC(60;84;120):{ 2;4;6;12}
nhưng vì x_> 6 nên x = 2,4,6
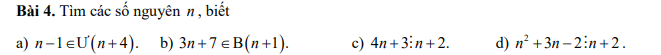

 Giúp vs ạ, gấp ạ, cảm ơn trc! Trình bày đầy đủ
Giúp vs ạ, gấp ạ, cảm ơn trc! Trình bày đầy đủ Giúp vs ạ, cần gấp, cảm ơn trc! Trình bày đầy đủ
Giúp vs ạ, cần gấp, cảm ơn trc! Trình bày đầy đủ

 giúp e bài 4 câu d e f ạ lm đầy đủ các bước e sẽ k nhé
giúp e bài 4 câu d e f ạ lm đầy đủ các bước e sẽ k nhé 






 các bạn giúp mik trc 7h tối nay nha. Mik tick cho bạn nào nhanh và đúng nhé
các bạn giúp mik trc 7h tối nay nha. Mik tick cho bạn nào nhanh và đúng nhé
b: \(\Leftrightarrow n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-2;1;-3;3;-5\right\}\)
c: \(\Leftrightarrow n+2\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{-1;-3;3;-7\right\}\)
d: \(\Leftrightarrow n+2\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{-1;-3;0;-4;2;-6\right\}\)
a: \(\Leftrightarrow n-1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{2;0;6;-4\right\}\)