Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


có [x-y]2=1
suy ra [x-y]mũ 2= 1 mũ 2
suy ra x-1=1
x=1+1
x=2

245a chia hết cho 5
120b chia hết cho 5
Nên \(245a+120b\)chia hết cho 5.
Mà 28764 không chia hết cho 5
Vậy không tồn tại số tự nhiên a,b nào để \(245a+120b=28764\)
Chúc bạn học tốt.

Lời giải:
Vì $a,b$ là số tự nhiên nên $2a+1,b-2$ là số nguyên
$(2a+1)(b-2)=12$ nên $2a+1$ là ước của $12$
Mà $2a+1$ là số tự nhiên lẻ nên $2a+1\in\left\{1;3\right\}$
Nếu $2a+1=1$ thì $b-2=12:1=12$
$\Rightarrow a=0; b=14$ (thỏa mãn)
Nếu $2a+1=3$ thì $b-2=12:3=4$
$\Rightarrow a=1; b=6$ (thỏa mãn)

=>2ab-3a+b-9=0
=>b(2a+1)-3a-4,5-*4,5=0
=>b(2a+1)-1,5(2a+1)=4,5
=>(2a+1)(b-1,5)=4,5
=>(2a+1)(2b-3)=9
=>\(\left(2a+1;2b-3\right)\in\left\{\left(1;9\right);\left(3;3\right);\left(9;1\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(0;6\right);\left(1;3\right);\left(4;2\right)\right\}\)

a . Ta có : \(n+10⋮n+1\)
\(n+1+9⋮n+1\)
mà\(n+1⋮n+1\)
\(\Rightarrow9⋮n+1\)
\(\Rightarrow n+1\inƯ\left(9\right)=\left\{1;3;9\right\}\)
Ta có bảng sau :
| n +1 | 1 | 3 | 9 |
| n | 0 | 2 | 8 |
để n+10 chia hết n+1 thì
9chia hết cho n+1
=>n+1 \(\inƯ\left(9\right)=\left\{1;3;9\right\}\)
ta có bảng sau
| n+1 | 1 | 3 | 9 |
| n | 2 | 4 | 10 |
| tm | tm | tm |
vậy...

Bạn dùng phương pháp chặn `b` rồi tìm `a` nhé.
`8a^2 + 31b^2 = 2468 <=> 31b^2 <= 2468 <=> b^2 < 81 -> b = 1 -> 8.`
Từ đây tìm `a` theo `b` và nhớ thử lại nhé.
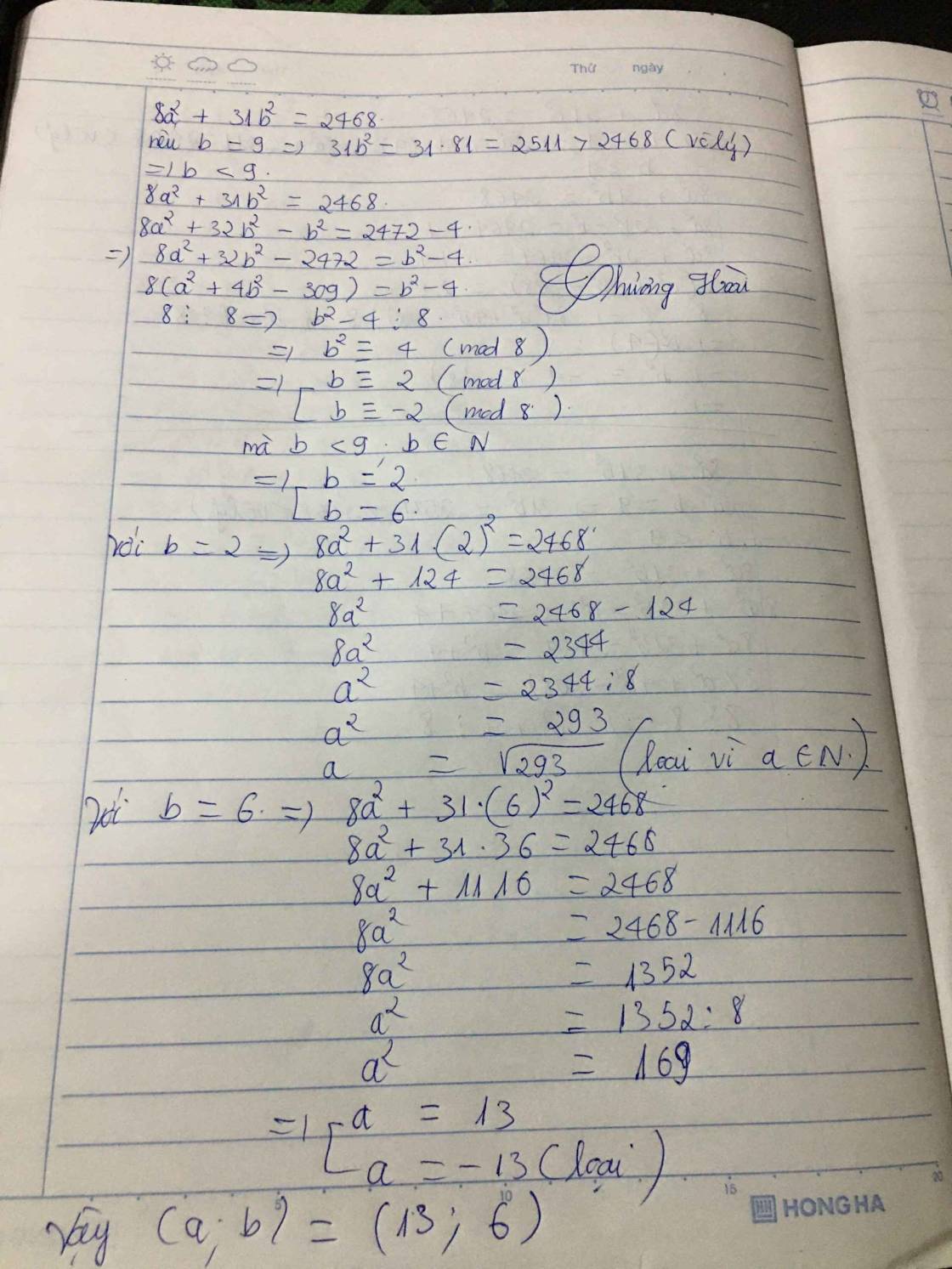
de UCLN cua a b = 24 thi a=24 hoac b=24
neu a=24 thi b=336-24=312
neu b=24 thi a=336-24=312
ma a<b suy ra a=24 va b = 312
a+b=24+312=336
UCLN (a,b) = UCLN (24 , 312 ) = 24
Ta có : a+b = 336
UCLN(a,b)=24 => a=24m, b = 24n với m,n khác 0 và UCLN (m,n) = 1
=> a + b = 24 ( m+ n ) = 336
m +n = 336 : 24 = 14
Lập bảng giá tri:
m 1 2 3 4 5 6 7 8 9 10 11 12 13
n 13 12 11 10 9 8 7 6 5 4 3 2 1
loại L L L L L L
a= m. 24 24 72 120 216 264 312
b = n.24 312 264 216 120 72 24
bạn tự kết luận nhé!
chú ý các giá tri bị loại do vi phạm điều kiện UCLN ( m,n) = 1