
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3^{x+4}=9^{2x-1}\)
\(\Rightarrow3^{x+4}=3^{4x-2}\)
\(\Rightarrow x+4=4x-2\)
\(\Rightarrow3x=6\Rightarrow x=2\)

c: ⇔n+2∈{1;−1;5;−5}⇔n+2∈{1;−1;5;−5}
hay n∈{−1;−3;3;−7}n∈{−1;−3;3;−7}
d: ⇔n+2∈{1;−1;2;−2;4;−4}⇔n+2∈{1;−1;2;−2;4;−4}
hay n∈{−1;−3;0;−4;2;−6}n∈{−1;−3;0;−4;2;−6}
a: ⇔n−1∈{1;−1;5;−5}⇔n−1∈{1;−1;5;−5}
hay n∈{2;0;6;−4}
b: \(\Leftrightarrow n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-2;1;-3;3;-5\right\}\)
c: \(\Leftrightarrow n+2\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{-1;-3;3;-7\right\}\)
d: \(\Leftrightarrow n+2\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{-1;-3;0;-4;2;-6\right\}\)
a: \(\Leftrightarrow n-1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{2;0;6;-4\right\}\)



Bài 4:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{x+y}{4+3}=\dfrac{14}{7}=2\)
Do đó: x=8; y=6
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{2x+3y}{2\cdot8+3\cdot12}=\dfrac{13}{52}=\dfrac{1}{4}\)
Do đó: x=2; y=3
a) \(\dfrac{x}{5}=\dfrac{2}{5}.\Rightarrow x=2.\)
b) \(\dfrac{3}{x-5}=\dfrac{-4}{x+2.}.\left(x\ne5;x\ne-2\right).\)
\(\Leftrightarrow\dfrac{3}{x-5}+\dfrac{4}{x+2}=0.\Leftrightarrow\dfrac{3x+6+4x-20}{\left(x-5\right)\left(x+2\right)}=0.\)
\(\Rightarrow7x-14=0.\Leftrightarrow x=2\left(TM\right).\)
c) \(\dfrac{x}{-2}=\dfrac{-8}{x}.\left(x\ne0\right).\Leftrightarrow\dfrac{-x}{2}+\dfrac{8}{x}=0.\Leftrightarrow\dfrac{-x^2+16}{2x}=0.\Rightarrow-x^2+16=0.\Leftrightarrow x^2=16.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=4^2.\\x^2=\left(-4\right)^2.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4.\\x=-4.\end{matrix}\right.\)\(\left(TM\right).\)
d) \(\dfrac{x+2}{5}=\dfrac{45}{x+2}.\left(x\ne-2\right).\)
\(\Leftrightarrow\dfrac{x+2}{5}-\dfrac{45}{x+2}=0.\Leftrightarrow\dfrac{x^2+4x+4-225}{5x+10}=0.\Rightarrow x^2+4x-221=0.\)
\(\Leftrightarrow\left(x-13\right)\left(x+17\right)=0.\Leftrightarrow\left[{}\begin{matrix}x-13=0.\\x+17=0.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=13.\\x=-17.\end{matrix}\right.\) \(\left(TM\right).\)

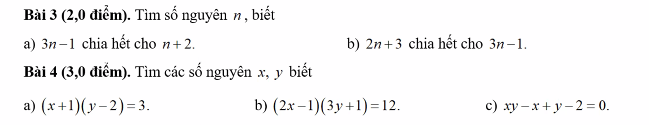
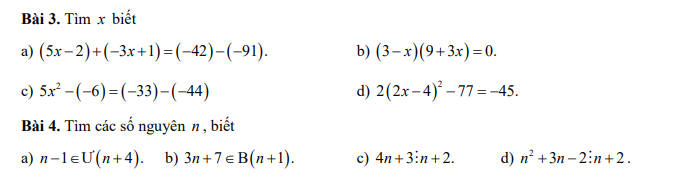
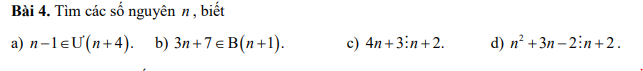
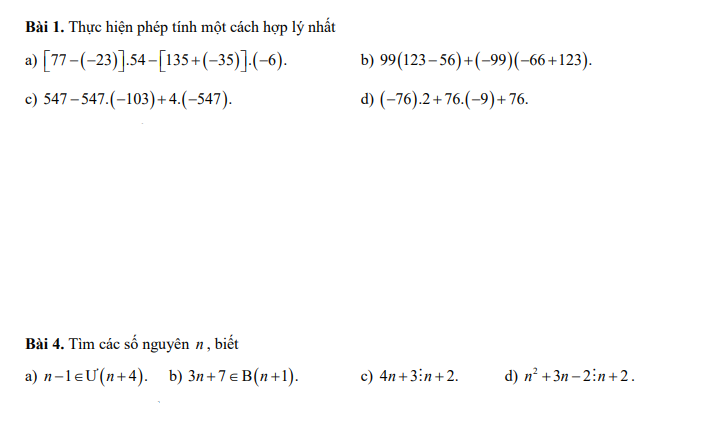
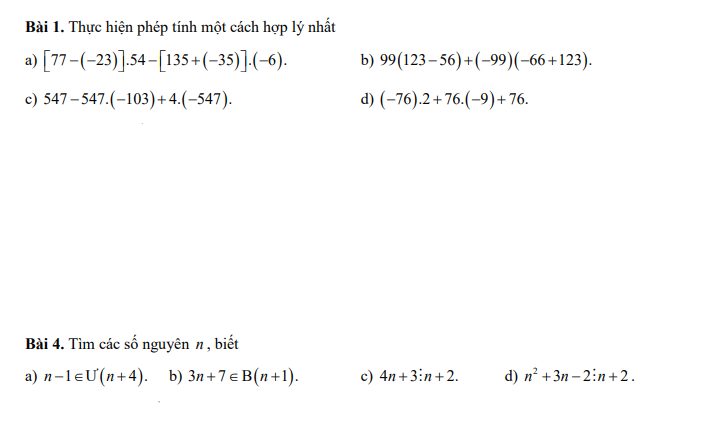 Các bạn làm nhanh và đầy đủ hộ mình nhé :))
Các bạn làm nhanh và đầy đủ hộ mình nhé :))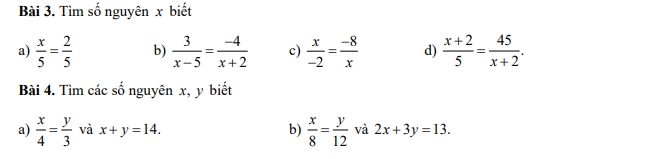

 Đaay nhé
Đaay nhé
Bài 3:
a: \(\Leftrightarrow n+2\in\left\{1;-1;7;-7\right\}\)
hay \(n\in\left\{-1;-3;5;-9\right\}\)