HT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 10 2018
Ta có \(\frac{a}{d}=\frac{c}{b}\Rightarrow\frac{b}{d}=\frac{c}{a}=\frac{c+b}{a+d}\)
Vậy C là phương án đúng
HT
1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
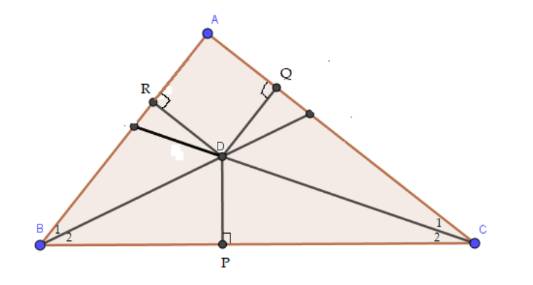
a) Vì BD là tia phân giác của góc ABC nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)
Vì CD là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)
Xét \(\Delta BDP\) vuông tại P và \(\Delta BDR\) vuông tại R, ta có:
\(\widehat {{B_2}} = \widehat {{B_1}}\)
BD chung
\( \Rightarrow \Delta BDP = \Delta BDR\) ( cạnh huyền – góc nhọn)
\( \Rightarrow \) DP = DR ( 2 cạnh tương ứng) (1)
b) Xét \(\Delta CDP\) vuông tại P và \(\Delta CDQ\) vuông tại Q, ta có:
\(\widehat {{C_2}} = \widehat {{C_1}}\)
CD chung
\( \Rightarrow \Delta CDP = \Delta CDQ\) ( cạnh huyền – góc nhọn)
\( \Rightarrow \) DP = DQ ( 2 cạnh tương ứng) (2)
c) Từ (1) và (2), ta được: DR = DQ ( cùng bằng DP).
D nằm trên tia phân giác của góc A do D cách đều AB và AC.
CM
5 tháng 7 2017
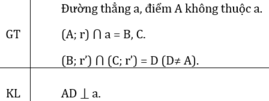
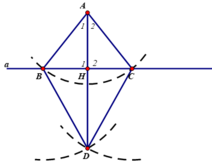
Gọi bán kính cung tròn tâm A là r, bán kính cung tròn tâm B và C là r’.
Xét ΔABD và ΔACD có:
AB = AC (=r)
DB = DC (=r')
AD cạnh chung
Nên ΔABD = ΔACD (c.c.c)
QUẢNG CÁO
- Gọi H là giao điểm của AD và a
ΔAHB và ΔAHC có
AB = AC (= r)
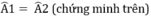
AH cạnh chung
⇒ ΔAHB = ΔAHC (c.g.c)
10 tháng 4 2020
∆ABD và ∆ACD có:
AB = AC (gt)
DB = DC (gt)
AD cạnh chung.
Nên ∆ABD = ∆ACD (c.c.c)
=> A1 = A2
Gọi H là giao điểm của AD và a.
∆AHB và ∆AHC có:
AB = AC (gt)
A1 = A2 ( cmt )
AH cạnh chung.
Nên ∆AHB = ∆AHC (c.g.c)
Suy ra: H1 = H2
Ta lại có:
H1 + H2 = 180
⇒H1 = H2 = 90
Vậy AD ⊥ a
10 tháng 4 2020
P/s : Cứ nghĩ làm xong bài sẽ vẽ hình ai ngờ phần vẽ hình bị lỗi nên lại phải làm lại ( khóc hết nước mắt )
Giải
Xét ∆ABD và ∆ACD có :
AB = AC (gt)
DB = DC (gt)
AD cạnh chung.
Nên ∆ABD = ∆ACD (c.c.c)
\(\Rightarrow\) BAD = CAD ( 2 góc tương ứng )
Gọi H là giao điểm của AD và a
Xét ∆AHB và ∆AHC có :
AB = AC (gt)
BAH = CAH ( cmt )
AH cạnh chung
Nên ∆AHB = ∆AHC (c.g.c)
\(\Rightarrow\) AHB = AHC ( 2 góc tương ứng )
Ta lại có :
AHB + AHC = 180 ( 2 góc kề bù )
\(\Rightarrow\) AHB = AHC = 90
\(\Rightarrow\) AH ⊥ BC
\(\Rightarrow\) AD ⊥ a
\(\frac{a}{b}=\frac{c}{d};a.d=c.b\)
\(a.d,b.c\),có nghĩa là quy đồng.Vì nếu quy đồng thì \(\frac{a}{b}=\frac{c}{d}=\frac{a.d}{b.d}=\frac{c.b}{d.b}\).
Ta thấy mẫu số quy đồng thì đương nhiên bằng nhau,mà tử số thì \(a.d=c.b\).
Vì \(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow\frac{a}{b}=\frac{c}{d};a.d=c.b\)là đúng.
Giải:
Ta có: a/d = b/c
⇒⇒ a/d : c/d = b/c : c/d
⇒⇒ a : c = d : d
⇒a/c=b/d⇒a/c=b/d
Vậy a/c=b/d