Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi D là trung điểm BC; E là trung điểm AC
Trong tam giác ABC có BC2 = AB2 + AC2 = 32 + 42 = 25
=> BC = 5
Trong tam giác vuông ABC có AD là đường trung tuyến ứng với cạnh huyền BC nên AD = BD = CD
mà BD = CD = BC/2 = 5/2 = 2,5 nên AD = 2,5
Ta có AG/AD = 2/3 => AG = (AD.2)/3 = (2,5 x 2)/3 = 5/3

∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
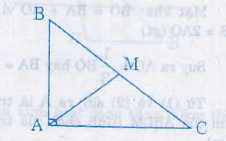
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = 1212 BC
Vì G là trọng tâm của ∆ ABC nên AG =2323 AM => AG =2323.1212 BC
=> AG = 1313 BC = 1313 .5 = 1.7cm

Gọi D là trung điểm BC; E là trung điểm AC
Trong tam giác ABC có BC2 = AB2 + AC2 = 32 + 42 = 25
=> BC = 5
Trong tam giác vuông ABC có AD là đường trung tuyến ứng với cạnh huyền BC nên AD = BD = CD
mà BD = CD = BC/2 = 5/2 = 2,5 nên AD = 2,5
Ta có AG/AD = 2/3 => AG = (AD.2)/3 = (2,5 x 2)/3 = 5/3

∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = BC
Vì G là trọng tâm của ∆ ABC nên AG = AM => AG =. BC
=> AG = BC = .5 = 1.7cm
B A C M
∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = BC
Vì G là trọng tâm của ∆ ABC nên AG = AM => AG =. BC
=> AG = BC = .5 = 1.7cm
hình vẽ không được đẹp bạn thông cảm nhé

tự vẽ hình ta vẽ AK là đường trung tuyến của cạnh huyền
xét tam giác ABC có:
AB2+AC2 = BC2 ( đ/lý py-ta-go)
=> 32 + 42 = BC2
=> 9 + 16 = BC2
=> BC = 25
=> BC = \(\sqrt{25}=5cm\)
tam giác ABC có AK là đường trung tuyến vs cạnh huyền => AK = \(\frac{BC}{2}=\frac{5}{2}=2,5\)
=> AG = \(\frac{2}{3}AK\) (đ/lý) => \(\frac{2}{3}x2,5=1,66666667\)
hình như mk làm sai hoặc bn sai đề
để ghi lại khúc cuối
AG = \(\frac{2}{3}AK=>\frac{2}{3}x\frac{5}{2}=\frac{5}{3}cm\)
có \(5:2=\frac{5}{2}\) nên mới có 5/2

+ Ta có \(BC^2=AB^2+AC^2=3^2+4^2=25\Rightarrow AC=5cm\)
+ Kẻ trung tuyến AM gọi G là trọng tâm cua tam giác ABC ta có
AG=2/3 AM mà AM=1/2 AC=2,5 cm => AG=(2/3).2,5=5/3 cm
ΔABC vuông tại A có BC2 = AB2 + AC2 (định lí Pitago)
⇒ BC2 = 32 + 42 = 25 ⇒ BC = 5 (cm)
Gọi M là trung điểm của BC ⇒ AM là trung tuyến.
Vì theo đề bài: trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên