Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có
f ' x = 3 x + a 2 + x + b 2 − x 2 = 3 x 2 + 2 a + b x + a 2 + b 2
Để hàm số luôn đồng biến trên − ∞ ; + ∞
thì Δ ' = a + b 2 − a 2 + b 2 ≤ 0 ⇔ a b ≤ 0
Ta có
P = a 2 + b 2 − 4 a − 4 b + 2 = a + b − 2 2 − 2 a b − 2 ≥ − 2.
Dâu bằng xảy ra khi a + b = 2 a b = 0 ⇔ a = 2 b = 0 hoặc ngược lại.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm xo∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho xo∈ (a;b) và f(xo)>f(x),∀x ∈ (a,b)∖{xo}.

Chọn đáp án D
Ta có
![]()
![]()
Suy ra
![]()
Từ giả thiết ta có f ' x + f ' ' x = 10 e x
![]()
Để phương trình f ' x + f ' ' x = 10 e x có nghiệm
⇔ Phương trình (*) có nghiệm
![]()
* Nếu b = 0 thì S = a 2 ≥ 10
* Nếu b ≠ 0 thì S = a 2 - 2 a b + 3 b 2 ≥ 10 . a b 2 - 2 . a b + 3 a b 2 + 1 .
Đặt t = a b t ∈ R , suy ra S ≥ 10 . t 2 - 2 t + 3 t 2 + 1 .
Xét hàm số f t = t 2 - 2 t + 3 t 2 + 1 trên R.
Ta có
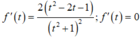
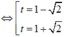
Bảng biến thiên:
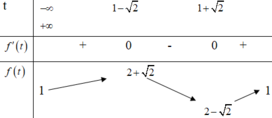
Quan sát bảng biến thiên ta thấy f t ≥ 2 - 2
![]()


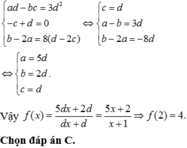

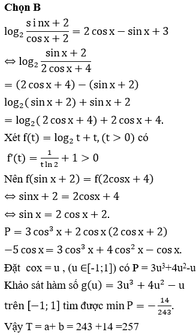
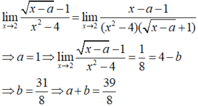
Đáp án B
Ta có: f ' x = − 3 x 2 + 3 x + a 2 + 3 x + b 2 = 3 x 2 + 6 a + b x + 3 a 2 + 3 b 2
Để hàm số đồng biến trên − ∞ ; + ∞ thì f ' x ≥ 0 ∀ x ∈ − ∞ ; + ∞
⇔ 3 x 2 + 6 a + b x + 3 a 2 + 3 b 2 ≥ 0 ∀ x ∈ ℝ ⇔ x 2 + 2 a + b x + a 2 + b 2 ≥ 0 ∀ x ∈ ℝ ⇔ Δ ' = a + b 2 − a 2 + b 2 ≤ 0 ⇔ 2 a b ≤ 0 ⇔ a b ≤ 0
TH1: b = 0 ⇒ P = a 2 − 4 a + 2 = a − 2 2 − 2 ≥ − 2 1
TH2: a > 0 , b < 0 ⇒ P = a − 2 2 + b 2 + − 4 b − 2 > − 2 2
Từ (1) và (2) ⇒ P min = − 2 k h i a = 0 hoặc b = 0.