HP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 4 2021
a)\(\dfrac{1}{2^2}<\dfrac{1}{1.2}\)
\(\dfrac{1}{3^3}<\dfrac{1}{2.3}\)
\(...\)
\(\dfrac{1}{8^2}<\dfrac{1}{7.8}\)
Vậy ta có biểu thức:
\(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{8^2}<\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{7.8}\)
\(B= 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{7}-\dfrac{1}{8}\)
\(B<1-\dfrac{1}{8}=\dfrac{7}{8}<1\)
Vậy B < 1 (đpcm)
27 tháng 4 2021
Giải:
a) Ta có:
1/22=1/2.2 < 1/1.2
1/32=1/3.3 < 1/2.3
1/42=1/4.4 < 1/3.4
1/52=1/5.5 < 1/4.5
1/62=1/6.6 < 1/5.6
1/72=1/7.7 < 1/6.7
1/82=1/8.8 <1/7.8
⇒B<1/1.2+1/2.3+1/3.4+1/4.5+1/5.6+1/6.7+1/7.8
B<1/1-1/2+1/2-1/3+1/3-1/4+1/4-1/5+1/5-1/6+1/6-1/7+1/7-1/8
B<1/1-1/8
B<7/8
mà 7/8<1
⇒B<7/8<1
⇒B<1
b)S=3/1.4+3/4.7+3/7.10+...+3/40.43+3/43.46
S=1/1-1/4+1/4-1/7+1/7-1/10+...+1/40-1/43+1/43-1/46
S=1/1-1/46
S=45/46
Vì 45/46<1 nên S<1
Vậy S<1
Chúc bạn học tốt!
NT
4
7 tháng 1 2016
Số số hạng của 12 + 22 + 32 + .. + 202 : (202 - 1) : 10 + 1 = 20
Số số hạng của 1 + 2 + 3 + .. + 20 : (20 - 1) + 1 = 20
S = {(12+ 202) - (1 + 20)} x 20 : 2 = 1930
Lúc nãy nhầm làm tổng của 2 dãy
D
1
L
28 tháng 4 2022
Đặt A=11⋅2+12⋅3+...+17⋅8A=11⋅2+12⋅3+...+17⋅8
Dễ thấy: B=122+132+...+182B=122+132+...+182<A=11⋅2+12⋅3+...+17⋅8(1)<A=11⋅2+12⋅3+...+17⋅8(1)
Ta có:A=11⋅2+12⋅3+...+17⋅8A=11⋅2+12⋅3+...+17⋅8
=1−12+12−13+...+17−18=1−12+12−13+...+17−18
=1−18<1(2)=1−18<1(2)
Từ (1);(2)(1);(2) ta có: B<A<1⇒B<1
5 tháng 4
a: Ta có
A = \(\dfrac{1}{10}\) + \((\dfrac{1}{11}\) + \(\dfrac{1}{12}\) + ...+ \(\dfrac{1}{100}\)\()\)
⇒ A > \(\dfrac{1}{10}\) + \((\dfrac{1}{100}\) + \(\dfrac{1}{100}\) + ...+ \(\dfrac{1}{100}\)\()\)90 số hạng
⇒ A > \(\dfrac{1}{10}\) + \(\dfrac{90}{100}\)
⇒ A > 1
vậy A > 1
b: ta có
S = (\(\dfrac{1}{21}\) + \(\dfrac{1}{22}\)+ \(\dfrac{1}{23}\) + \(\dfrac{1}{24}\) + \(\dfrac{1}{25}\))+(\(\dfrac{1}{26}\) + \(\dfrac{1}{27}\)+ \(\dfrac{1}{28}\) + \(\dfrac{1}{29}\) + \(\dfrac{1}{30}\))+(\(\dfrac{1}{31}\) + \(\dfrac{1}{32}\)+ \(\dfrac{1}{33}\) + \(\dfrac{1}{34}\) + \(\dfrac{1}{35}\))
⇒ S > (\(\dfrac{1}{25}\) + \(\dfrac{1}{25}\)+ \(\dfrac{1}{25}\) + \(\dfrac{1}{25}\) + \(\dfrac{1}{25}\))+(\(\dfrac{1}{30}\) + \(\dfrac{1}{30}\)+ \(\dfrac{1}{30}\) + \(\dfrac{1}{30}\) + \(\dfrac{1}{30}\))+(\(\dfrac{1}{35}\) + \(\dfrac{1}{35}\)+ \(\dfrac{1}{35}\) + \(\dfrac{1}{35}\) + \(\dfrac{1}{35}\))
⇔ S > \(\dfrac{5}{25}\)+\(\dfrac{5}{30}\)+\(\dfrac{5}{35}\)
⇔ S > \(\dfrac{1}{5}\)+\(\dfrac{1}{6}\)+\(\dfrac{1}{7}\)
⇔ S > \(\dfrac{107}{210}\)> \(\dfrac{105}{210}\)=\(\dfrac{1}{2}\)
vậy S > \(\dfrac{1}{2}\)
PT
4
8 tháng 7 2018
42-(2x+32)+12:2=6
42-2x-32+6=6
=> 42-32-2x=0
=> 10-2x=0
=>2x=10=> x=5
cái tính tổng thì theo công thức tính tổng: số đầu+số cuối)x số số hạng:2
số số hạng:(497-2):5+1=100
tổng là: 499x100:2
8 tháng 7 2018
\(1,42-\left(2x+32\right)+12:2=6\)
\(\Rightarrow42-2x-32=0\)
\(\Rightarrow10-2x=0\)
\(\Rightarrow2x=10\Leftrightarrow x=5\)
\(2,S=2+7+12+17+...+497\)
\(\Rightarrow S=\frac{\left(497+2\right)\left[\left(497-2\right):5+1\right]}{2}\)
\(\Rightarrow S=\frac{499.100}{2}=499.50\)
\(\Rightarrow S=24950\)
12 tháng 8 2023
a)\(...A=\dfrac{2^{50+1}-1}{2-1}=2^{51}-1\)
b) \(...\Rightarrow B=\dfrac{3^{80+1}-1}{3-1}=\dfrac{3^{81}-1}{2}\)
c) \(...\Rightarrow C+1=1+4+4^2+4^3+...+4^{49}\)
\(\Rightarrow C+1=\dfrac{4^{49+1}-1}{4-1}=\dfrac{4^{50}-1}{3}\)
\(\Rightarrow C=\dfrac{4^{50}-1}{3}-1=\dfrac{4^{50}-4}{3}=\dfrac{4\left(4^{49}-1\right)}{3}\)
Tương tự câu d,e,f bạn tự làm nhé
PT
1
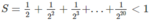
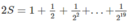
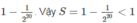
đề sai rồi bạn