Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Định lý Pitago đã học ở lớp 7, trong chương trình lớp 8 lẽ ra không cần giải thích lại?
Đặt 1 cạnh góc vuông của tam giác là \(\overline{ab}\) thì cạnh huyền là \(\overline{ba}\), với a;b là các chữ số từ 1 đến 9 và \(a>b\)
Đặt cạnh góc vuông còn lại là \(c\Rightarrow10\le c< 99\)
Theo định lý Pitago:
\(\left(\overline{ab}\right)^2+c^2=\left(\overline{ba}\right)^2\Leftrightarrow\left(10a+b\right)^2+c^2=\left(10b+a\right)^2\)
\(\Leftrightarrow100a^2+20ab+b^2+c^2=100b^2+20ab+a^2\)
\(\Leftrightarrow c^2=99\left(b^2-a^2\right)\)
\(\Rightarrow c^2⋮99\) \(\Rightarrow c\) chia hết cho 2 ước nguyên tố của 99 là 3 và 11
\(\Rightarrow c⋮33\Rightarrow c=\left\{33;66\right\}\)
- Với \(c=33\Rightarrow b^2-a^2=11\Leftrightarrow\left(b-a\right)\left(b+a\right)=11\)
\(\Rightarrow\left\{{}\begin{matrix}b-a=1\\b+a=11\end{matrix}\right.\) \(\Rightarrow a=5;b=6\)
- Với \(c=66\Rightarrow b^2-a^2=44\Rightarrow\left(b-a\right)\left(b+a\right)=44\)
\(\Rightarrow\left(a;b\right)=\left(10;12\right)\) đều lớn hơn 9 (loại)
Vậy 3 cạnh của tam giác vuông đó là 33; 56; 65
Đến đây thì 1 vấn đề xuất hiện, lớp 8 chưa học đường tròn, đường tròn nội tiếp thì càng không, vậy làm sao để tính bán kính đường tròn nội tiếp tam giác?

Bài 8: Vì em nhắn tin nhờ cô giảng bài 8 nên cô chỉ giảng bài 8 thôi nhé
Gọi các cạnh góc vuông, cạnh huyền của tam giác cần tìm lần lượt là: a; b; c
Theo bài ra ta có: a+b+c =36; \(\dfrac{a}{b}\) = \(\dfrac{3}{4}\)
\(\dfrac{a}{b}\) = \(\dfrac{3}{4}\) ⇒ \(\dfrac{a}{3}\) = \(\dfrac{b}{4}\) ⇒ \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{a^2+b^2}{9+16}\) (1)
Vì tam giác vuông nên ta theo pytago ta có: a2 + b2 = c2 (2)
Thay (2) vào (1) ta có: \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{c^2}{25}\)
⇒ \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) = \(\dfrac{a+b+c}{3+4+5}\) = \(\dfrac{36}{12}\) = 3
a = 3.3 = 9 (cm)
b = 3.4 = 12 (cm)
c = 3.5 = 15 (cm)
Kết luận: độ dài cạnh bé của góc vuông là: 9 cm
dộ dài cạnh lớn của góc vuông là 12 cm
độ dài cạnh huyền là 15 cm

Bài 9:
a,Gọi độ dài cạnh góc vuông là: a
Theo pytago ta có: a2 + a2 = 22 = 4 ⇒ 2a2 = 4 ⇒ a2 = 2 ⇒ a = \(\sqrt{2}\)
b, Gọi độ dài cạnh góc vuông là :b
Theo pytago ta có:
b2 + b2 = 102 =100 ⇒ 2b2 = 100 ⇒ b2 = 50⇒ b = 5\(\sqrt{2}\)
Bài 8 cô làm rồi nhé.
Bài 10 ; Gọi độ dài các cạnh góc của tam giác vuông lần lượt là:
a; b theo bài ra ta có:
\(\dfrac{a}{5}\) = \(\dfrac{b}{12}\) \(\Rightarrow\) \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{a^2+b^2}{25+144}\) (1)
Theo pytago ta có: a2 + b2 = 522 = 2704 (2)
Thay (2) vào (1) ta có: \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{2704}{169}\) = 16
⇒ a2 = 25.16 = (4.5)2 ⇒ a = 20
b2 = 144.16 = (12.4)2 ⇒ b = 48

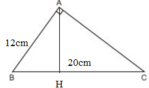
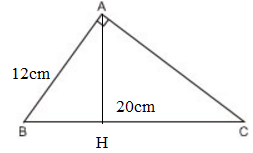
ΔABC vuông tại A có đường cao AH, BC = 20cm, AB = 12cm. Ta tính HC.
ΔABC và ΔHBA có:
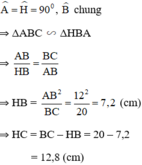

Gọi độ dài cạnh góc vuông còn lại là x
=>ĐỘ dài cạnh huyền là x+3
THeo đề, ta có: x^2+25=(x+3)^2
=>x^2+6x+9=x^2+25
=>6x=16
=>x=8/3
=>\(S=\dfrac{8}{3}\cdot3\cdot\dfrac{1}{2}=4\left(cm^2\right)\)

Xét hai tam giác vuông DAC và DBA ,ta có:
∠ (ADC) = ∠ (BDA) = 90 0
∠ C = ∠ (DAB) (hai góc cùng phụ ∠ B )
Suy ra: △ DAC đồng dạng △ DBA (g.g)
Suy ra: 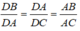
⇒ D A 2 = D B . D C
hay DA = D B . D C = 9 . 16 = 12 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
A B 2 = D A 2 + D B 2 = 9 2 + 12 2 = 225 ⇒ AB =15 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACD,ta có:
AC2 = DA2 + DC2 = 122 +162 = 400 ⇒ AC = 20cm
Vậy BC = BD + DC = 9 + 16 = 25(cm)
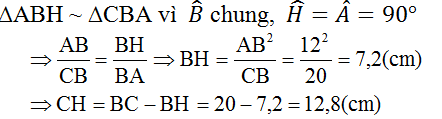
\(R=\dfrac{a+b}{2}\)