Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Áp dụng định luật bảo toàn cơ năng xác định được vận tốc của hệ ngay sau khi va chạm là . Từ đó áp dụng định luật bảo toàn động lượng xác định được vận tốc của đạn (lúc đầu vận tốc của túi cát là 0), tức là
, từ đó suy ra v.
b. Áp dụng định luật bảo toàn năng lượng suy ra lượng năng lượng đã chuyển hóa thành nhiệt năng là bằng hiệu cơ năng của hệ lúc đầu và lúc sau, tức là

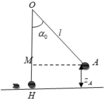
a. Chọn mốc thế năng là vị trí cân bằng của bao cát
Vận tốc của bao cát và viên đạn ngay sau khi va chạm. Theo định luật bảo toàn cơ năng
W H = W A ⇒ 1 2 ( m + m 0 ) V H 2 = ( m + m 0 ) g z A M à z A = l − l cos 60 0 = l ( 1 − cos 60 0 ) ⇒ V H = 2 g l ( 1 − c o s 60 0 ) = 2.10.2 ( 1 − 1 2 ) = 2 5 ( m / s )
Theo định luật bảo toàn động lượng
m 0 v 0 = ( m + m 0 ) V H ⇒ v 0 = ( m + m 0 ) V H m 0 = ( 19 , 9 + 0 , 1 ) .2 5 0 , 1 = 400 5 ( m / s )
b. Độ biến thiên động năng
Δ W d = W d 2 − W d 1 = m + m 0 2 ( m 0 v 0 m + m 0 ) 2 − m 0 v 0 2 2 ⇒ Δ W d = ( m 0 m + m 0 − 1 ) m 0 v 0 2 2 = − m m + m 0 . m 0 . v 0 2 2
⇒ Δ W d = − 19 , 9 19 , 9 + 0 , 1 . 0 , 1. ( 400 5 ) 2 2 = − 39800 ( J )
Vậy năng lượng được chuyển hóa thành nhiệt năng là 39800 J

Hệ vật gồm "Đầu đạn - Hộp cát - Trái Đất" là một hệ cô lập, vì không có các ngoại lực (lực cản, lực ma sát) tác dụng. Do đó, động lượng và cơ năng của hệ vật bảo toàn. Chọn mặt đất làm gốc tính thế năng trọng trường và chiều chuyển động của các vật là chiều dương
- Áp dụng định luật bảo toàn động lượng cho quá trình va chạm mềm khi đầu đạn bay tới xuyên vào hộp cát theo phương ngang, ta có :
(m + M)V = mv ⇒ V = mv/(m+M)
trong đó v là vận tốc của đầu đạn có khối lượng m, còn V là vận tốc của hộp cát chứa đầu đạn có tổng khối lượng M + m.
- Áp dụng định luật bảo toàn cơ năng cho quá trình khi hộp cát chứa đầu đạn có vận tốc V chuyển động trong trọng trường và trọng tâm của nó được nâng cao thêm một đoạn h so với vị trí cân bằng, ta có :
(m + M)gh = (m + M) V 2 /2 ⇒ V = 2 g h
Từ hai phương trình trên, ta suy ra vận tốc của đầu đạn :
v = (m + M)/m . 2 g h = 249,5(m/s)

a) Ta có: \(v_2=0m/s\)
Gọi vận tốc sau va chạm là: \(v\)
Áp dụng định luật bảo toàn động lượng:
\(m_1v_1+m_2v_2=\left(m_1+m_2\right)v\)
\(\Leftrightarrow m_1v_1=\left(m_1+m_2\right)v\)
\(\Leftrightarrow v=\dfrac{m_1v_1}{m_1+m_2}=\dfrac{0,12.580}{0,12+45}\approx1,45m/s\)
b) Ta có: \(v_2=1,2m/s\)
Áp dụng định luật bảo toàn động lượng ta có:
\(m_1v_1+m_2.v_2=\left(m_1+m_2\right)v\)
\(\Leftrightarrow v=\dfrac{m_1v_1+m_2.v_2}{m_1+m_2}\)
\(\Leftrightarrow v=\dfrac{0,12.580+45.1,2}{0,12+45}\approx2,74m/s\)
c) Ta có: \(v_2=1,5m/s\)
Do bao cát chuyển động ngược chiều, áp dụng định luật bảo toàn động lượng:
\(m_1v_1-m_2v_2=\left(m_1+m_2\right)v\)
\(\Leftrightarrow v=\dfrac{m_1v_1-m_2v_2}{m_1+m_2}\)
\(\Leftrightarrow v=\dfrac{0,12.580-45.1,5}{0,12+45}\approx0,05m/s\)

Lời giải
Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của viên đạn
Gọi v 1 , v 2 , V lần lượt là vận tốc viên đạn, xe lúc trước là xe lúc sau va chạm. Ta có:
m 1 v 1 + m 2 v 2 = m 1 + m 2 V ⇒ V = m 1 v 1 + m 2 v 2 m 1 + m 2 ⇔ 7 , 4 = m 1 .600 − 1 , 5.0 , 5 m 1 + 1 , 5 ⇔ m 1 = 0 , 02 k g = 20 g
Với v 2 = − 0 , 5 m / s vì xe chuyển động ngược chiều so với viên đạn
Đáp án: A

chọn mốc thế năng tại điểm thấp nhất ( trùng với phương bay của đạn )
Vật chỉ chịu tác dụng của trọng lực cơ năng được bảo toàn: ( Bảo toàn cho hệ lúc vừa cắm vào bao cát đến lúc bao cát lên 1 đoạn h=0,8(m) )
a) \(W_1=W_2\Leftrightarrow\dfrac{1}{2}\left(m+M\right)v_1^2=\left(m+M\right)gz_2\) \(\Rightarrow v_1=\sqrt{\dfrac{2\left(m+M\right)gz_2}{m+M}}=4\left(m/s\right)\)
b) Bảo toàn động lượng:
\(mv_0=\left(m+M\right)v_1\Rightarrow v_0=\dfrac{\left(m+M\right)v_1}{m}=704\left(m/s\right)\)