Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABN và ΔACM có
AB=AC
\(\widehat{BAN}\) chung
AN=AM
Do đó: ΔABN=ΔACM
b: Ta có: AM+MB=AB
AN+NC=AC
mà AM=AN và AB=AC
nên MB=NC
Xét ΔMBC và ΔNCB có
MB=NC
\(\widehat{MBC}=\widehat{NCB}\)
BC chung
Do đó: ΔMBC=ΔNCB
=>\(\widehat{BMC}=\widehat{CNB}\) và \(\widehat{MCB}=\widehat{NBC}\)
Ta có: \(\widehat{MCB}=\widehat{NBC}\)
=>\(\widehat{OCB}=\widehat{OBC}\)
=>ΔOBC cân tại O
=>OB=OC
c: Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Ta có: FB=FC
=>F nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,F thẳng hàng

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

a, xét hai tam giác ABM và ACM có AB=AC, MB=MC, AM chung \(\Rightarrow\) ABM=ACM (c.c.c)
b, AB=AC nên ABC là tam giác cân, M là trung điểm BC nên AM vuông góc với BC
c,xét 2 tam giác AEH và CEM có EA=EC, EM=EH, góc MEC= góc HEA nên hai tam giác đó bằng nhau (c.g.c)
d, theo câu c đã có tam giác AEH=CEM nên góc AHE= góc CME. Hai góc này ở vị trí so le nên AH // BC (1)
tiếp tục xét 2 tam giác DKA và DMB, có góc KDA=DBM, DK = DM. Mặt khác ta thấy DMEA là hinhf bình hành nên ME=AD=DB ( do ME cũng là đường trung bình của ABC)
nên suy ra tam giác DKA=DMB suy ra góc AKD=BMD, hai góc này ở vị trí so le nên AK// BC(2)
Từ 1 và 2 suy ra AH và AK cùng nằm trên 1 đường thẳng hay K,H,A thẳng hàng...

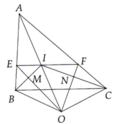
a: Xét ΔABN và ΔACM có
AB=AC
góc BAN chung
AN=AM
Do đo: ΔABN=ΔACM
b: Xét ΔMBC và ΔNCB có
MB=NC
góc MBC=góc NCB
BC chung
Do đó: ΔMBC=ΔNCB
=>góc OBC=góc OCB
=>OB=OC
c: ΔABC cân tại A
mà AF là trung tuyến
nên AF là trung trực của BC
mà O nằm trên trung trực của BC
nên A,O,F thẳng hàng