Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

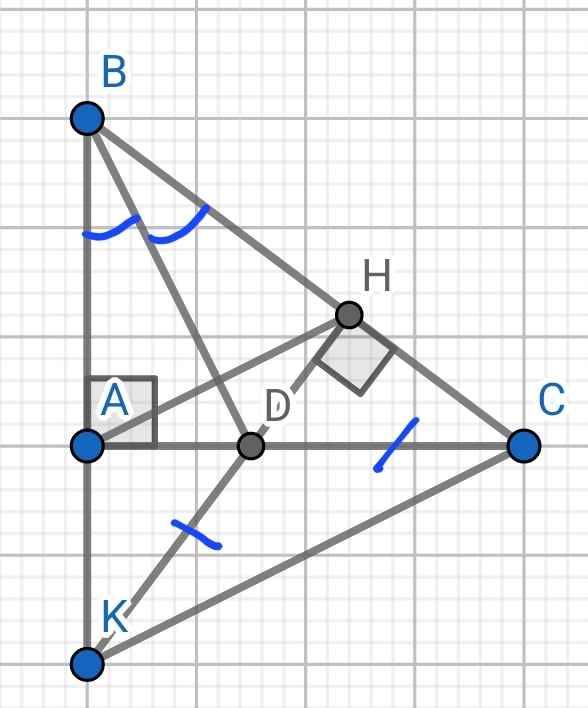
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:
BD chung
∠ABD = ∠HBD (BD là phân giác của ∠ABH)
⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆HBD (cmt)
⇒ AB = BH (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABD = ∆HBD (cmt)
⇒ AD = HD (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AH
c) Xét ∆ADK và ∆HDC có:
AD = HD (cmt)
∠ADK = ∠HDC (đối đỉnh)
DK = DC (gt)
⇒ ∆ADK = ∆HDC (c-g-c)
⇒ ∠DAK = ∠DHC (hai góc tương ứng)
⇒ ∠DAK = 90⁰
Mà ∠DAB = 90⁰
⇒ ∠DAK + ∠DAB = 180⁰
⇒ B, A, K thẳng hàng

a: Xét ΔABD vuông tạiA và ΔHBD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: BA=BH
DA=DH
=>BD là trung trực của AH
c: Xét ΔDAK và ΔDHC có
DA=DH
góc ADK=góc HDC
DK=DC
=>ΔDAK=ΔDHC
=>góc DAK=góc DHC=90 độ
=>góc DAK+góc DAB=180 độ
=>B,A,K thẳng hàng

Xét tam giác ABD và tam giác HBD có:
BD: chung.
Góc BAD=BHD=90 độ.
Góc ABD=HBD(Phân giác BD)
=> Tam giác ABD=tam giác HBD(ch-gn)
b/ Gọi giao điểm của BD và AH là O.
Xét tam giác AOB và tam giác HOB có:
BO:chung.
Góc ABO=HBO(Phân giác BD)
BA-BH(cạnh tương ứng của tam giác BAD=BHD)
=>Tam giác AOB=tam giác HOB(c-g-c)
=> Góc AOB=HOB(góc tương ứng)=90 độ
Góc BAH=BKC(góc ứng với cạnh đáy của tam giác cân có cùng góc B)
=> AH//KC
Mà BD vuông góc với AH nên BD cũng vuông góc với KC.
c/Xét tam giác ADK và tam giác HDC có:
DA=DH(cạnh tương ứng của tam giác BAD=tam giác BHD)
Góc DAK=DHC=90 độ.
Góc ADK=HDC(đối đỉnh)
=> tam giác ADK=tam giác HDC(g-c-g)
=> DK=DC(cạnh tương ứng)
Mà trong tam giác vuông HDC có:
DC là cạnh huyền nên DC>DH
=> DK>DH(đpcm)
=> tự vẽ hình nha .


a) Xét △ABC vuông tại A có:
BC² = AC² + AB² (ĐL Pytago)
BC² = 8² + 6²
BC² = 100
BC = 10 cm
Vậy BC = 10 cm
b) Xét △ABD và △EBD có:
góc BAD = góc BED (=90°)
BD chung
góc ABD = góc EBD (BD là tia p/g của góc ABC)
=> △ABD = △EBD (ch-gn)
c) Câu này đề bài có cho thiếu gia thiết ko bạn chứ vẽ hình chả biết ntn á

a) Xét 2 tam giác vuông ABD và HBD ta có:
BD là cạnh chung
góc ABD = góc HBD (BD là đường phân giác của góc B)
\(\Rightarrow\Delta ABD=\Delta HBD\) (canh huyền - góc nhọn)

5 )
tự vẽ hình nha bạn
a)
Xét tam giác ABM và tam giác ACM có :
AM cạnh chung
AB = AC (gt)
BM = CM (gt)
suy ra : tam giác ABM = tam giác ACM ( c-c-c)
suy ra : góc BAM = góc CAM ( 2 góc tương ứng )
Hay AM là tia phân giác của góc A
b)
Xét tam giác ABD và tam giác ACD có :
AD cạnh chung
góc BAM = góc CAM ( c/m câu a)
AB = AC (gt)
suy ra tam giác ABD = tam giác ACD ( c-g-c)
suy ra : BD = CD ( 2 cạnh tương ứng)
C) hay tam giác BDC cân tại D
Xét \(\Delta ABD\)và \(\Delta HBD\)ta có :
\(\widehat{ABD}=\widehat{HBD}\)( Vì BD là tia phân giác ) (1)
\(BD:\)Cạnh chung (2)
\(\widehat{BAD}=\widehat{BHD}=90^o\) (3)
Từ (1) ;(2) và (3)
\(\Rightarrow\Delta ABD=\Delta HBD\)( góc - cạnh-góc)
b) Vì \(\Delta ABD=\Delta HBD\)( Chứng minh ở câu a)
\(\Rightarrow AB=HB\)( Cặp cạnh tương ứng )
\(\Rightarrow\Delta ABH\)Cân (1)
Ta lại có : BD là phân giác (2)
Từ (1) và (2)
=> BD là đường trung trực của AH
( Vì trong 1 tam giác cân đường phân giác ứng với cạnh đáy đồng thời là đường trung trực)
c) Vì \(\Delta ABD=\Delta HBD\)( Chứng minh câu a )
\(\Rightarrow AD=HD\)( Cặp cạnh tương ứng )
Xét \(\Delta ADK\)và \(\Delta HDC\)ta có :
\(\widehat{KDA}=\widehat{CDH}\)( đối đỉnh ) (1)
\(AD=HD\)(Chứng minh trên) (2)
\(\widehat{KAD}=\widehat{CHD}=90^o\)(GT ) (3)
Từ (1);(2) và (3)
\(\Rightarrow\Delta ADK=\Delta HDC\)( Góc - cạnh góc )
\(\Rightarrow DK=DC\)( Cặp cạnh tương ứng )
d) Áp dụng định lí Py-ta-go ta có :
\(AB^2+AC^2=BC^2\)
\(6^2+8^2=BC^2\)
\(36+64=BC^2\)
\(\Rightarrow100=BC^2\)
\(\Rightarrow BC=\sqrt{100}\)
\(\Rightarrow BC=10\)
Vì AB=HB ( Chứng minh ở câu b)
Mà \(AB=6cm\)
\(\Rightarrow HB=6cm\)
Ta có : \(HB+HC=BC\)
\(\Rightarrow6+HC=10\)
\(\Rightarrow HC=10-6\)
\(\Rightarrow HC=4cm\)