K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
1
23 tháng 12 2023
a: ĐKXĐ: \(x\notin\left\{1;-1;-2\right\}\)
b: \(N=\left(\dfrac{1}{x+1}+\dfrac{1}{x-1}+\dfrac{x^2}{x^2-1}\right)\cdot\dfrac{x-1}{x+2}\)
\(=\left(\dfrac{1}{x+1}+\dfrac{1}{x-1}+\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{x-1}{x+2}\)
\(=\dfrac{x-1+x+1+x^2}{\left(x+1\right)\left(x-1\right)}\cdot\dfrac{x-1}{x+2}\)
\(=\dfrac{x^2+2x}{\left(x+2\right)\left(x+1\right)}=\dfrac{x}{x+2}\)
c: |x|=2
=>x=2(nhận) hoặc x=-2(loại)
Thay x=2 vào N, ta được:
\(N=\dfrac{2}{2+2}=\dfrac{2}{4}=\dfrac{1}{2}\)
AH
Akai Haruma
Giáo viên
26 tháng 8 2023
13.
$(x+4)^2+(x+5)(x-5)-2x(x+1)$
$=(x^2+8x+16)+(x^2-25)-(2x^2+2x)$
$=x^2+8x+16+x^2-25-2x^2-2x$
$=(x^2+x^2-2x^2)+(8x-2x)+(16-25)=6x-9$
14.
$(x-1)^2-2(x+3)(x-3)+4x(x-4)$
$=(x^2-2x+1)-2(x^2-9)+(4x^2-16x)$
$=x^2-2x+1-2x^2+18+4x^2-16x$
$=(x^2-2x^2+4x^2)+(-2x-16x)+(1+18)=3x^2-18x+19$
15.
$(y-3)(y+3)(y^2+9)-(y^2+2)(y^2-2)$
$=(y^2-9)(y^2+9)-(y^4-4)$
$=(y^4-81)-(y^4-4)=-81+4=-77$
29 tháng 6 2023
a: =12x^4-6x^3+3x+4x^3-2x^2+1
=12x^4-2x^3-2x^2+3x+1
b: =14x^4+28x^2+6x^2+12x
=14x^4+34x^2+12x
29 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
\((3x + 1)(4x³ - 2x² + 1)\)
`= 3x(4x^3-2x^2+1) + 4x^3 - 2x^2 + 1`
`= 12x^4 - 6x^3 + 3x + 4x^3 - 2x^2 + 1`
`= 12x^4 + (-6x^3 + 4x^3) - 2x^2 + 3x + 1`
`= 12x^4 - 2x^3 - 2x^2 + 3x + 1`
\((7x² + 3x)(2x + 4)\)
`= 7x^2(2x+4) + 3x(2x+4)`
`= 14x^3 + 28x^2 + 6x^2 + 12x`
`= 14x^3 + (28x^2 + 6x^2)+12x`
`= 14x^3 + 34x^2 + 12x`
`@` `\text {Kaizuu lv uuu}`
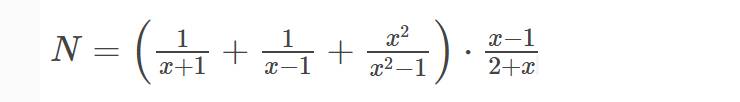
biểu thức nào?
biểu thức đâu?
biểu thức ÙwÚ
máy lỗi