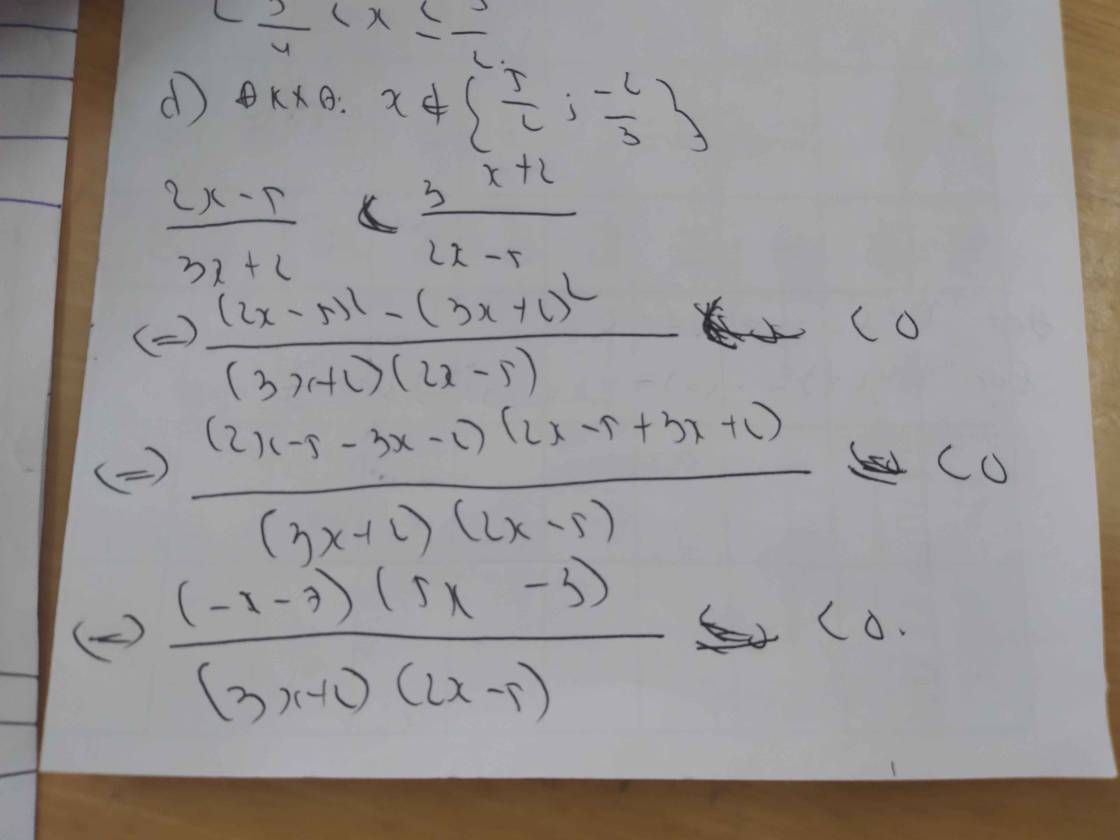Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số xác định trên R khi và chỉ khi:
a.
\(\left(2m-4\right)x+m^2-9=0\) vô nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}2m-4=0\\m^2-9\ne0\end{matrix}\right.\) \(\Rightarrow m=2\)
b.
\(x^2-2\left(m-3\right)x+9=0\) vô nghiệm
\(\Leftrightarrow\Delta'=\left(m-3\right)^2-9< 0\)
\(\Leftrightarrow m^2-6m< 0\Rightarrow0< m< 6\)
c.
\(x^2+6x+2m-3>0\) với mọi x
\(\Leftrightarrow\Delta'=9-\left(2m-3\right)< 0\)
\(\Leftrightarrow m>6\)
e.
\(-x^2+6x+2m-3>0\) với mọi x
Mà \(a=-1< 0\Rightarrow\) không tồn tại m thỏa mãn
f.
\(x^2+2\left(m-1\right)x+2m-2>0\) với mọi x
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(2m-2\right)=m^2-4m+3< 0\)
\(\Leftrightarrow1< m< 3\)

a) \(\left(x+1\right)\left(x-1\right)\left(3x-6\right)>0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-1< x< 1\\x>2\end{matrix}\right.\)
b) \(\dfrac{x+3}{x-2}\le0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow-3\le x< 2\)
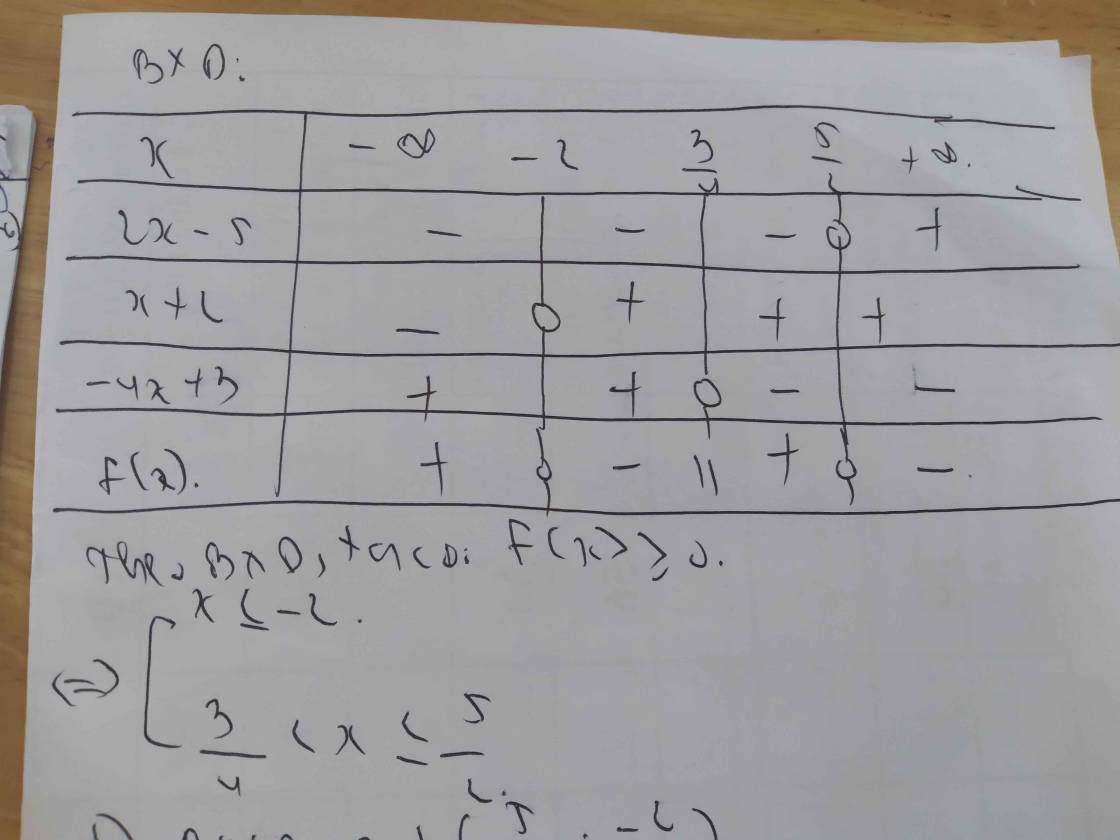
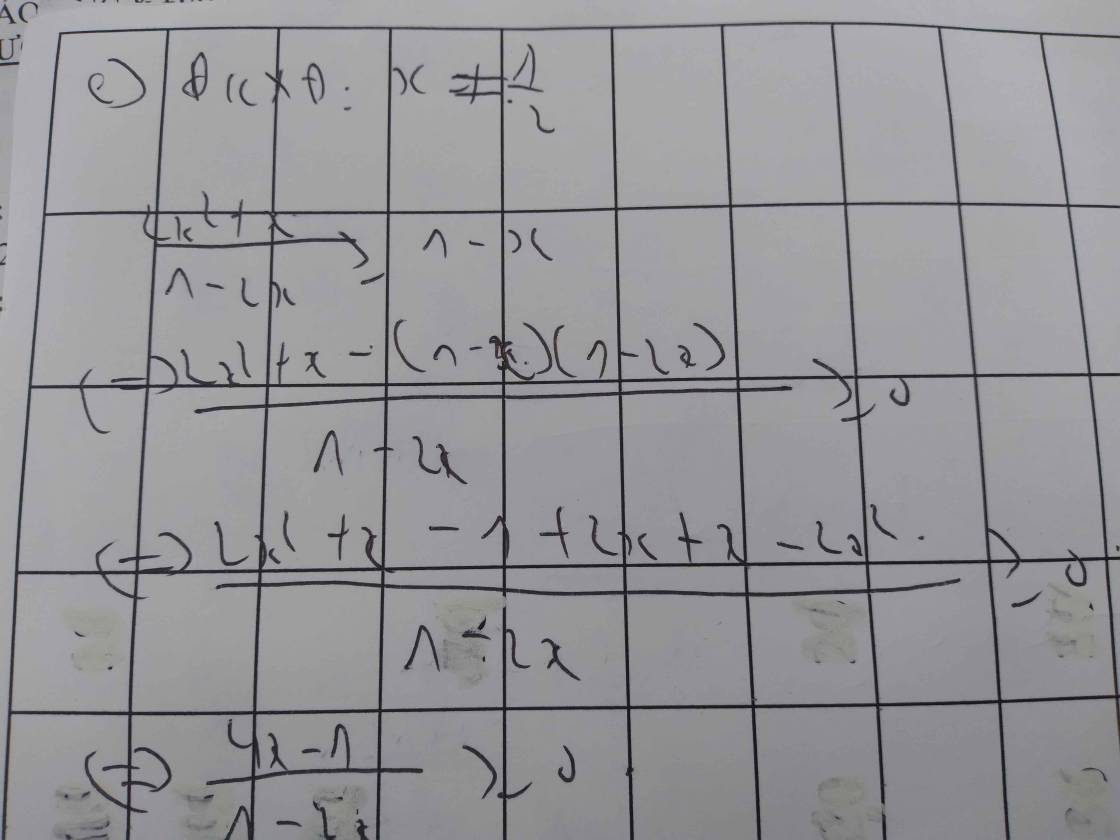
d) \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
\(\Leftrightarrow\dfrac{2x-5}{3x+2}-\dfrac{3x+2}{2x-5}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5\right)^2-\left(3x+2\right)^2}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5+3x+2\right)\left(2x-5-3x-2\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
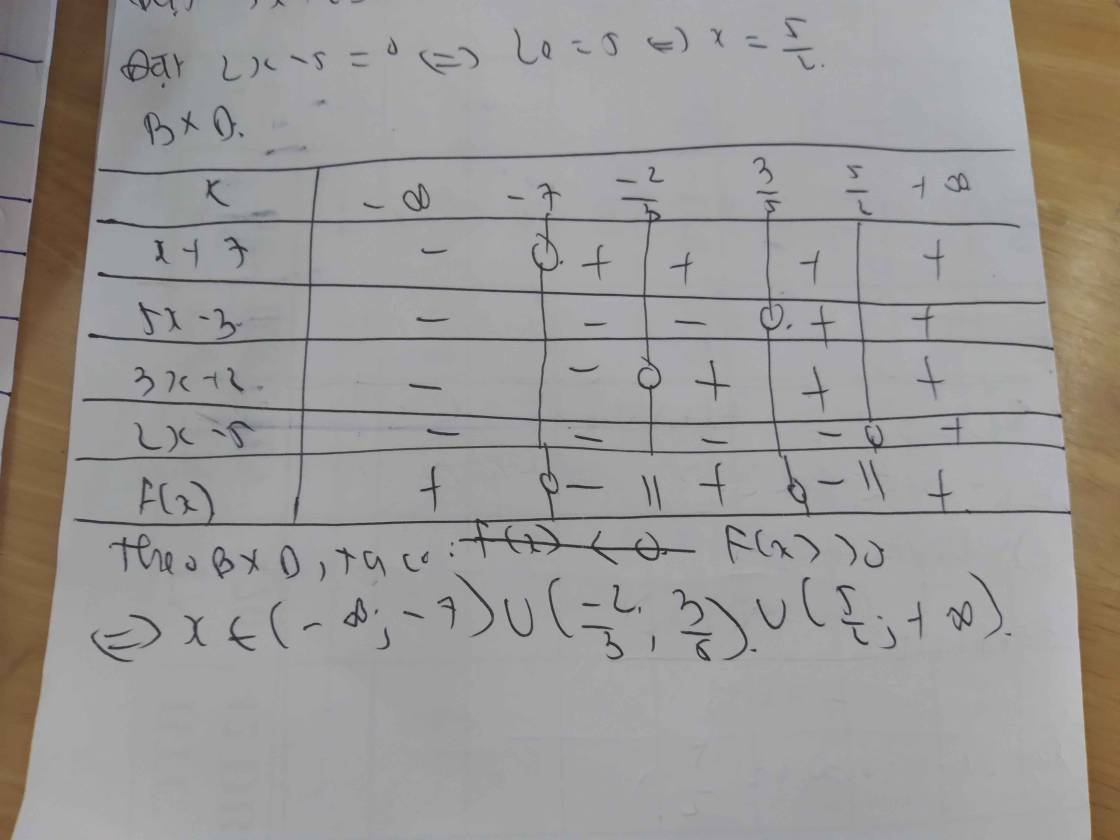
\(\Leftrightarrow\dfrac{-\left(5x-3\right)\left(x+7\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-7< x< -\dfrac{2}{3}\\\dfrac{5}{3}< x< \dfrac{5}{2}\end{matrix}\right.\)

1:
c: =>1/3x+2/3-x+1>x+3
=>-2/3x+5/3-x-3>0
=>-5/3x-4/3>0
=>-5x-4>0
=>x<-4/5
d: =>3/2x+5/2-1<=1/3x+2/3+x
=>3/2x+3/2<=4/3x+2/3
=>1/6x<=2/3-3/2=-5/6
=>x<=-5
2:





a) TXĐ: \(D=R\).
b) \(TXD=D=R\backslash\left\{4\right\}\)
c) Đkxđ: \(\left\{{}\begin{matrix}4x+1\ge0\\-2x+1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{-1}{4}\\x\le\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\dfrac{-1}{4}\le x\le\dfrac{1}{2}\).
TXĐ: D = \(\left[\dfrac{-1}{4};\dfrac{1}{2}\right]\)
a) Đkxđ: \(\left\{{}\begin{matrix}x+9\ge0\\x^2+8x-20\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-9\\\left\{{}\begin{matrix}x\ne2\\x\ne-10\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-9\\x\ne2\end{matrix}\right.\)
Txđ: D = [ - 9; 2) \(\cup\) \(\left(2;+\infty\right)\)
b) Đkxđ: \(\left\{{}\begin{matrix}2x+1\ne0\\x-3\ne0\end{matrix}\right.\Leftrightarrow\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{-1}{2}\\x\ne3\end{matrix}\right.\)
Txđ: \(D=R\backslash\left\{\dfrac{-1}{2};3\right\}\)
c) \(x^2+2x-5\ne0\Leftrightarrow\left\{{}\begin{matrix}x\ne-1+\sqrt{6}\\x\ne-1-\sqrt{6}\end{matrix}\right.\)
Txđ: \(D=R\backslash\left\{-1+\sqrt{6};-1-\sqrt{6}\right\}\)

a. ĐKXĐ: \(x\ge-1\)
\(y=\sqrt{x^3+1+2\sqrt{x^3+1}+1}+\sqrt{x^3+1-2\sqrt{x^3+1}+1}\)
\(=\sqrt{\left(\sqrt{x^3+1}+1\right)^2}+\sqrt{\left(\sqrt{x^3+1}-1\right)^2}\)
\(=\left|\sqrt{x^3+1}+1\right|+\left|1-\sqrt{x^3+1}\right|\ge\left|\sqrt{x^3+1}+1+1-\sqrt{x^3+1}\right|=2\)
b.
\(f\left(x\right)=\dfrac{x-1}{2}+\dfrac{2}{x-1}+\dfrac{1}{2}\ge2\sqrt{\dfrac{2\left(x-1\right)}{2\left(x-1\right)}}+\dfrac{1}{2}=\dfrac{5}{2}\)
c.
\(y=\dfrac{x-2018+1}{\sqrt{x-2018}}=\sqrt{x-2018}+\dfrac{1}{\sqrt{x-2018}}\ge2\sqrt{\dfrac{\sqrt{x-2018}}{\sqrt{x-2018}}}=2\)

c ơi cái này là toán 7, thi học kì 1 mà, bọn em cũng đn ôn đề này á

e: \(f\left(-x\right)=\dfrac{\left(-x\right)^4+3\cdot\left(-x\right)^2-1}{\left(-x\right)^2-4}=\dfrac{x^4+3x^2-1}{x^2-4}=f\left(x\right)\)
Vậy: f(x) là hàm số chẵn
\(c,f\left(-x\right)=\sqrt{-2x+9}=-f\left(x\right)\)
Vậy hàm số lẻ
\(d,f\left(-x\right)=\left(-x-1\right)^{2010}+\left(1-x\right)^{2010}\\ =\left[-\left(x+1\right)\right]^{2010}+\left(x-1\right)^{2010}\\ =\left(x+1\right)^{2010}+\left(x-1\right)^{2010}=f\left(x\right)\)
Vậy hàm số chẵn
\(g,f\left(-x\right)=\sqrt[3]{-5x-3}+\sqrt[3]{-5x+3}\\ =-\sqrt[3]{5x+3}-\sqrt[3]{5x-3}=-f\left(x\right)\)
Vậy hàm số lẻ
\(h,f\left(-x\right)=\sqrt{3-x}-\sqrt{3+x}=-f\left(x\right)\)
Vậy hàm số lẻ