Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
+ Chia đều 10 đội vào 2 bảng A và B có ![]() cách.
cách.
Do đó số phần tử của không gian mẫu là : ![]()
+ Sắp xếp đội của lớp 10A1 và 10A2 vào 2 bảng khác nhau A và B có 2! cách.
Chọn 4 đội trong 8 đội còn lại để xếp vào bảng có đội lớp 10A1 có C 8 4 cách.
Bốn đội còn lại xếp vào bảng còn lại.
Suy ra số cách chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau là ![]()
Gọi A là biến cố “Chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau ” thì số các kết quả thuận lợi cho biến cố A là: ![]()
+ Xác suất cần tìm là: 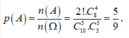

Tham khảo:
Giá trị nhỏ nhất là: 5.
Giá trị lớn nhất là 54.
Do đó khoảng biến thiên là 54 - 5 = 49.
Để chia thành 6 nhóm với độ dài bằng nhau ta lấy điểm đầu mút phải trái của nhóm đầu tiên là 3 và đầu mút phải của nhóm cuối cùng là 57 với độ dài mỗi nhóm là 9.
Ta được mẫu số liệu ghép nhóm như sau:


Đáp án : D
Thứ 2 : có 9 cách chọn bạn đi thăm
Thứ 3 : có 9 cách chọn bạn đi thăm
Thứ 4 : có 9 cách chọn bạn đi thăm
Thứ 5 : có 9 cách chọn bạn đi thăm
Thứ 6 : có 9 cách chọn bạn đi thăm
Thứ 7 : có 9 cách chọn bạn đi thăm
Chủ nhật : có 9 cách chọn bạn đi thăm
Vậy theo quy tắc nhân, có (kế hoạch)

Không gian mẫu: \(C_9^3.C_6^3\)
Chia 3 bạn nữ vào 3 tổ: \(3!\) cách
Xếp 6 bạn nam vào 3 tổ: \(C_6^2.C_4^2\) cách
Xác suất: \(P=\dfrac{3!.C_6^2.C_4^2}{C_9^3.C_6^3}\)

Một tuần có bảy ngày và mỗi ngày thăm một bạn.
Có 12 cách chọn bạn vào ngày thứ nhất.
Có 11 cách chọn bạn vào ngày thứ hai ( khác bạn ngày thứ nhất).
Có 10 cách chọn bạn vào ngày thứ ba ( khác bạn ngày thứ nhất, thứ 2)
Có 9 cách chọn bạn vào ngày thứ tư.
Có 8 cách chọn bạn vào ngày thứ năm.
Có 7 cách chọn bạn vào ngày thứ sáu.
Có 6 cách chọn bạn vào ngày thứ bảy.
Vậy theo qui tắc nhân ta có 12.11.10.9.8.7.6 = 3 991 680 cách.
Chọn đáp án A.

Khi chọn 1 nhóm thì nhóm kia hoàn toàn xác định (vì là những người còn lại).
Sậy số cách chia hai nhóm bằng số cách chọn ra 1 nhóm có 9 người hoặc 10 người, trong đó có 5 hoặc 6 nữ.
Ta có:
-Số cách chọn 10 người, trong đó có 5 nữ bằng số cách chọn 5 nam từ 8 nam và 5 nữ từ 11 nữ và bằng \(C_8^5.C_{11}^5\)
-Số cách chọn 9 người, trong đó có 5 nữ bằng số cách chọn 4 nam từ 8 nam và 5 nữ từ 11 nữ và bằng \(C_8^4.C_{11}^5\)
-Số cách chọn 10 người, trong đó có 6 nữ bằng số cách chọn 4 nam từ 8 nam và 6 nữ từ 11 nữ và bằng \(C_8^4.C_{11}^6\)
-Số cách chọn 9 người, trong đó có 6 nữ bằng số cách chọn 3 nam từ 8 nam và 6 nữ từ 11 nữ và bằng \(C_8^3.C_{11}^6\)
Tổng số cách chọn là: \(C_8^5.C_{11}^5\)+ \(C_8^4.C_{11}^5\)+ \(C_8^4.C_{11}^6\) + \(C_8^3.C_{11}^6\)

Đáp án: C
Một tuần có bảy ngày và mỗi ngày thăm một bạn.
Có 10 cách chọn bạn vào ngày thứ nhất.
Có 9 cách chọn bạn vào ngày thứ hai.
Có 8 cách chọn bạn vào ngày thứ ba.
Có 7 cách chọn bạn vào ngày thứ tư.
Có 6 cách chọn bạn vào ngày thứ năm.
Có 5 cách chọn bạn vào ngày thứ sáu.
Có 4 cách chọn bạn vào ngày thứ bảy.
Vậy theo qui tắc nhân ta có 10.9.8.7.6.5.4=604800 cách.

Đáp án D
Tổng số cách chọn 8 em từ đội 18 người là ![]()
Số cách chọn 8 em từ khối 12 và khối 11 là ![]()
Số cách chọn 8 em từ khối 11 và khối 10 là ![]()
Số cách chọn 8 em từ khối 10 và khối 12 là ![]()
Vậy số cách chọn để có các em ở cả 3 khối là
![]()
Một ngày 40 người đắp được số phần công việc là: 1:15=1/15(công việc)
Sau 3 ngày thì 40 người làm được số phần công việc là: 1/15x3=1/5(công việc)
40 người gấp 20 người: 40:20=2(lần)
1 ngày 20 người làm được số phần công việc là: 1/15:2=1/30 (công việc)
số công việc còn lại sau 3 ngày là: 1-1/5=4/5(công việc)
20 người phải làm thêm : 4/5:1/30=24(ngày)
Đội CN đó đắp xong đoạn đường được giao trong: 24+3=27(ngày)