Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

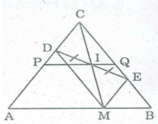
Gọi C là giao điểm của AD và BE.
Tam giác ABC có:
∠ A = 60 0 (vì ΔADM đều)
∠ B = 60 0 ( vì ΔBEM đều)
Nên ∠ C = 180 0 - ∠ A - ∠ B = 60 0
Suy ra: ∆ ABC đều hay AB = AC = BC
Suy ra điểm C cố định.
Lại có: ∠ A = ∠ (EMB ) = 60 0
ME // AC ( vì có cặp góc đồng vị bằng nhau)
Hay ME // CD.
Do ∠ DMA = ∠ BEM = 60 0 ( hai tam giác AMD và BME là tam giác đều )
Suy ra: MD // BC ( vì có cặp góc so le trong bằng nhau ).
hay MD // EC
suy ra tứ giác CDME là hình bình hành.
I là trung điểm của DE nên I là trung điểm của CM
Kẻ CH ⊥ AB,IK ⊥ AB⇒IK // CH
Trong ∆ CHM,ta có:CI = IM và IK // CH
Suy ra IK là đường trung bình của ΔCHM⇒IK = 1/2 CH
Vì C cố định nên CH không đổi ⇒ IK = 1/2 CH không đổi nên I chuyển động trên đường thẳng song song với AB, cách AB một khoảng bằng 1/2 CH
Khi M trùng với A thì I trùng với trung điểm P của AC.
Khi M trùng với B thì I trùng với trung điểm Q của BC.
Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ ( P là trung điểm AC, Q là trung điểm BC).

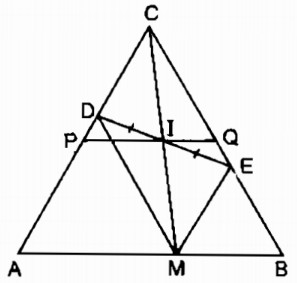
Gọi giao điểm của AD và BE là C.
∆ ABC có: ˆA=600A^=600 (vì ∆ ADM đều)
ˆB=600B^=600 (vì ∆ BEM đều)
Suy ra: ∆ ABC đều, AC = AB = BC nên điểm C cố định
ˆA=ˆEMB=600A^=EMB^=600
⇒ ME // AC (vì có cặp góc đồng vị bằng nhau)
hay ME // DC
ˆDMA=ˆB=600DMA^=B^=600
⇒ MD // BC (vì có cặp góc đồng vị bằng nhau)
hay MD // EC
Tứ giác CDME là hình bình hành
I là trung điểm của DE nên I là trung điểm của CM
Kẻ CH ⊥ AB, IK ⊥ AB ⇒ IK // CH
Trong ∆ CHM ta có:
CI = IM
IK // CH
nên IK là đường trung bình của ∆ CHM ⇒ IK = 1212CH
C cố định ⇒ CH không đổi ⇒ IK =1212CH không thay đổi nên I chuyển động trên đường thẳng song song AB, cách AB một khoảng bằng 1212CH.
Khi M trùng với A thì I trùng trung điểm P của AC.
Khi M trùng với B thì I trùng với trung điểm Q của BC.
Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ (P là trung điểm của AC, Q là trung điểm của BC)
Xem thêm tại: http://sachbaitap.com/cau-129-trang-96-sach-bai-tap-sbt-toan-8-tap-1-c6a8515.html#ixzz4zLYSfxii

a/ Từ I hạ IE vuông góc AB; Từ K hạ KF vuông góc AB
+ Xét tg vuông AMN
IE vuông góc AB; MN vuông góc AB => IE//MN
IA=IN
=> IE là đường trung bình của tg AMN => IE = MN/2
+ Xét tg vuông BMP chứng minh tương tự => KF//MN và KF = MP/2
Mà MN=AM và MP=MB
=> IE=AM/2 và KF=MB/2
+ Xét tư giác IEFK có IE//MN; KF//MN (cmt) => IEFK là hình thang
Từ O hạ OH vuông góc AB => OH//E//KF
mà OI=OK
=> OH là đường trung bình của hình thang IEFK
=> \(OH=\frac{IE+FK}{2}=\frac{\frac{AM}{2}+\frac{MB}{2}}{2}=\frac{AM+MB}{4}=\frac{AB}{4}=\frac{6}{4}=1,5cm\)
b/ Xét tg vuông BMP có MP=MB => tg BMP cân tại M
M=90
=> ^MPB=^MBP=45
Chứng minh tương tự khi xét tg vuông AMN => ^MAN=^MNA=45
+ Xét tg ABC có ^NAM=^MBP=45 => tg ABC cân tại C
Ta có A; B cố định
^CAB=CBA=45
=> C cố định
c/ Ta có OH=AB/4 (cmt) mà AB=6 là hằng số => OH không đổi => O luôn cách AB 1 khoảng cố định không đổi =AB/4
=> O chạy trên đường thẳng //AB và cách AB 1 khoảng không đổi = AB/4
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập v
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
ào trang web.