Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: góc MIC=góc MEC=90 độ
=>MIEC nội tiếp
2: Xet ΔMCQ và ΔMAC có
góc MCQ=góc MAC
góc CMQ chung
=>ΔMCQ đồng dạng với ΔMAC
=>MC/MA=MQ/MC
=>MC^2=MQ*MA

a) Xét tứ giác ECOM có
\(\widehat{OME}\) và \(\widehat{OCE}\) là hai góc đối
\(\widehat{OME}+\widehat{OCE}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECOM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a, (O): góc BAC=90 độ (góc nt chắn nửa đường tròn).
(I): góc AEH=90(góc nt chắn nửa đường tròn). góc ADH=90(góc nt chắn nửa đường tròn) => tg AEHD là hcn(có 3 góc vuông)
b) (I): góc ADE=góc AHE( nt cùng chắn cung AE)
ta lại có:góc AHE=góc ABH( cùng phụ với góc BAH.) => ADE=ABH
=> tg BEDC nội tiếp (góc trong tại 1 đỉnh = góc ngoài tại đỉnh đối diện)
c, tg AEHD là hcn; AH cắt AD tại I => IA=IH=IE=ID
tam giác ADH: DI là trung tuyến
tam giác: AMH: MI là trung tuyến => D,M,I thẳng hàng. mà E,M,I thẳng hàng=> D,M,E thẳng hàng.
Nhớ L I K E nha

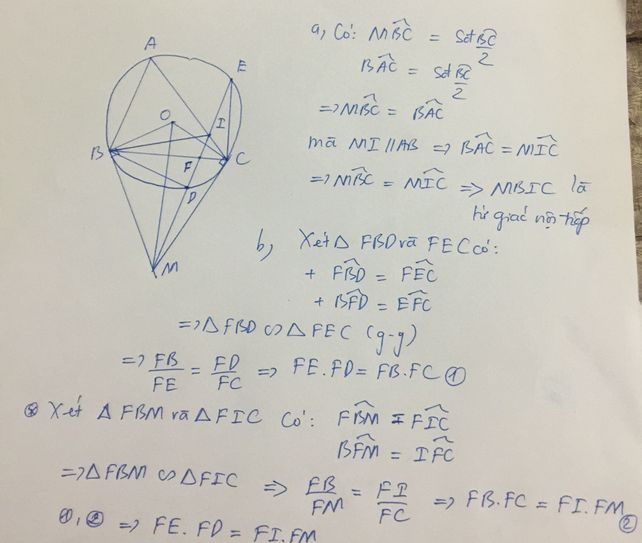 đây nha bn
đây nha bn
1: góc MIC+góc MEC=180 độ
=>MICE nội tiếp
2: Xét ΔMCQ và ΔMAC có
góc MCQ=góc MAC
góc CMQ chung
=>ΔMCQ đồng dạng với ΔMAC
=>MC^2=MQ*MA