
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét tứ giác AICO có
\(\widehat{IAO}+\widehat{ICO}=180^0\)
Do đó: AICO là tứ giác nội tiếp
hay A,I,C,O cùng thuộc 1 đường tròn
b: Xét (O) có
IA là tiếp tuyến có A là tiếp điểm
IC là tiếp tuyến có C là tiếp điểm
Do đó: IA=IC
Xét (O) có
KC là tiếp tuyến có C là tiếp điểm
KB là tiếp tuyến có B là tiếp điểm
Do đó: KC=KB
Ta có: IK=CI+CK
nên IK=IA+BK

b: \(=x-4\sqrt{x}+3\sqrt{x}-12=\left(\sqrt{x}-4\right)\left(\sqrt{x}+3\right)\)

Lời giải:
Theo định lý Viet:
$x_1+x_2=\frac{2}{2}=1$
$x_1x_2=\frac{-1}{2}$
Ta có:
$y_1+y_2=\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_1+x_2-2}{(x_1-1)(x_2-1)}$
$=\frac{x_1+x_2-2}{x_1x_2-(x_1+x_2)+1}=\frac{1-2}{\frac{-1}{2}-1+1}=2$
$y_1y_2=\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{x_1x_2-(x_1+x_2)+1}$
$=\frac{1}{\frac{-1}{2}-1+1}=-2$
Theo định lý Viet đảo, $y_1,y_2$ là nghiệm của pt:
$y^2-2y-2=0$
Lời giải:
Theo định lý Viet:
$x_1+x_2=\frac{2}{2}=1$
$x_1x_2=\frac{-1}{2}$
Ta có:
$y_1+y_2=\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_1+x_2-2}{(x_1-1)(x_2-1)}$
$=\frac{x_1+x_2-2}{x_1x_2-(x_1+x_2)+1}=\frac{1-2}{\frac{-1}{2}-1+1}=2$
$y_1y_2=\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{x_1x_2-(x_1+x_2)+1}$
$=\frac{1}{\frac{-1}{2}-1+1}=-2$
Theo định lý Viet đảo, $y_1,y_2$ là nghiệm của pt:
$y^2-2y-2=0$


a: Ta có: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{x-\sqrt{x}-1}{x-2\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}-\dfrac{x-5}{x-\sqrt{x}-2}\right)\)
\(=\dfrac{x-x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-2\right)}:\dfrac{x-4-x+5}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{1}\)
\(=\dfrac{x+2\sqrt{x}+1}{\sqrt{x}}\)


 bài 3 câu c help pls
bài 3 câu c help pls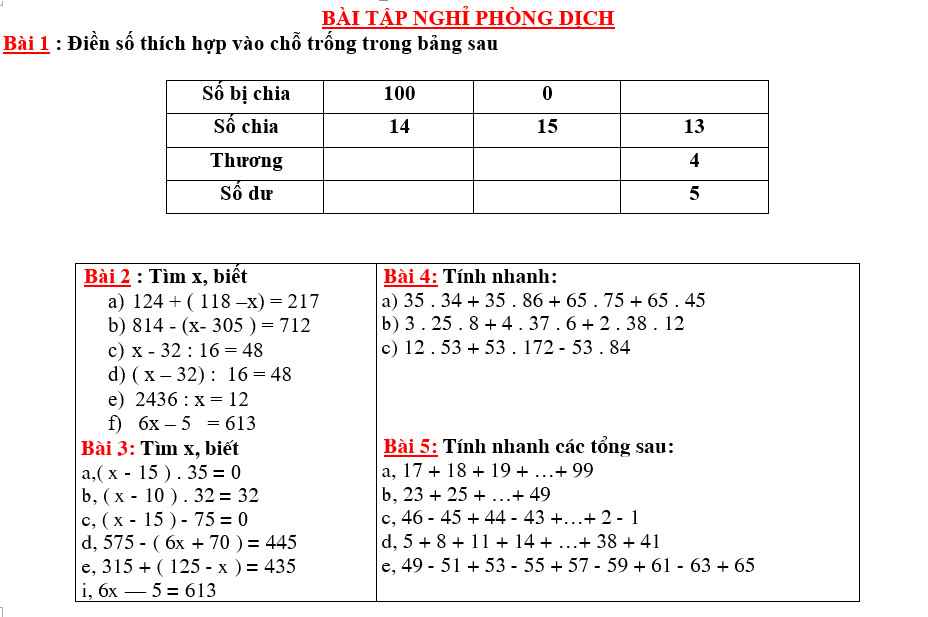

 help me pls
help me pls




Giả sử d cắt trục tung tại A ; trục hoành tại B
=> Tọa độ A(0;2) ; Tọa độ B(\(\left(\dfrac{-2}{m+3};0\right)\)
SAOB = 4
=> \(\dfrac{AO.OB}{2}=4\)
=> AO.OB = 8
<=> \(2.\dfrac{-2}{m+3}=8\)
<=> \(m=-\dfrac{7}{2}\)