Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\Delta ABC\) vuông tại A áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{BC^2+AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
Các tỉ số lượng giác của góc B là:
\(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\)
\(cosB=\dfrac{AB}{BC}=\dfrac{3}{5}\)
\(tanB=\dfrac{AC}{AB}=\dfrac{4}{3}\)
\(cotg=\dfrac{AB}{AC}=\dfrac{3}{4}\)
Các câu b), c) làm tương tự nhé
a: AC=căn 5^2-3^2=4cm
sin B=AC/BC=4/5
cos B=AB/BC=3/5
tan B=4/3
cot B=1:4/3=3/4
b: AB=căn 13^2-12^2=5cm
sin B=AC/BC=12/13
cos B=AB/BC=5/13
tan B=12/13:5/13=12/5
cot B=1:12/5=5/12
c: BC=căn 4^2+3^2=5cm
sin B=AC/BC=4/5
cos B=AB/BC=3/5
tan B=4/3
cot B=3/4

a) Áp dụng định lý Py-ta-go vào \(\Delta\)ABC ta có :
BC\(^2\)= AB\(^2\)+AC\(^2\)
=> AC\(^2\) = 25 - 9
=> AC = 4 (cm)
SinB = AC/BC = \(\frac{4}{5}\)
CosB = AB/BC = \(\frac{3}{5}\)
TanB = AC/AB =\(\frac{4}{3}\)
CotB =AB/AC = \(\frac{3}{4}\)
b) Áp dụng định lý Py-ta-go vào \(\Delta\)ABC có :
BC2 = AB2 +AC2
=> BC2= 169 +144
=> BC =\(\sqrt{313}\)
SinB = AC/BC =\(\frac{12}{\sqrt{313}}\)
CosB = AB/BC = \(\frac{13}{\sqrt{313}}\)
TanB = AC/AB =\(\frac{12}{13}\)
CotB = AB/AC = \(\frac{13}{12}\)

a) Ta có: \(BC=13cm\Rightarrow BC^2=13^2cm=169cm\)
Xét: \(AB^2+AC^2=5^2+12^2=25+144=169=13^2=BC^2\)
Vậy tam giác ABC vuông tại A có cạnh huyền BC
b) Áp dụng định lý thích hai cạnh góc vuông tà tích giữa cạnh huyền và đường cao ta có:
\(AH\cdot BC=AB\cdot AC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot5}{13}\approx4,6\left(cm\right)\)
c) Xét ΔAHB vuông tại H có đường cao HE ta có:
\(\Rightarrow AH^2=AE\cdot AB\) (1)
Xét ΔAHC vuông tại H có đường cao HF ta có:
\(\Rightarrow AH^2=AF\cdot AC\) (2)
Từ (1) và (2)
\(\Rightarrow AB\cdot AE=AC\cdot AF\)
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AC}{AE}\) (3)
Dựa vào (3)
Ta suy ra: \(\Delta AEF\sim\Delta ABC\)
\(\Rightarrow\widehat{AEF}=\widehat{ABC}\) (đpcm)
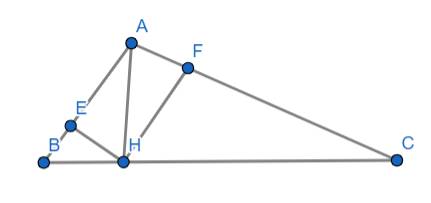
a: Xét ΔÂBC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
b: AH=AB*AC/BC=60/13(cm)
c: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
=>góc AFE=góc ABC

a,Sin B=\(\frac{AC}{BC}=\)\(\frac{4}{5}=0.8\)
Cos B=\(\frac{AB}{BC}=\frac{3}{5}=0,6\)
Tan B =\(\frac{AC}{AB}=\frac{4}{3}\)
Cot B=\(\frac{AB}{AC}=\frac{3}{4}=0,75\)
b,Vì sin B = 0,8 => B=53o
=> C=37o(áp dụng hệ quả định lí tổng r tính)

a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=12(cm)
b: Xét ΔBAC vuông tại A có
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{12}{13}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{5}{13}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{12}{5}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{5}{12}\)