Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

{(1999x2001-1)/(1998+1999x2000)}x7/5
={[(1999x(2000+1)-1]/(1998+1999x2000)}...
={(1999x2000+1999-1)/(1998+1999x2000)}...
={(1999x2000+1998)/(1998+1999x2000)}x7...
=1x7/5
=7/5

a. Ta tính trước số bị chia: 1 + 4 + 7 + …… + 100
Dãy số gồm có: (100 – 1) : 3 + 1 = 34 (số hạng)
Ta thấy: 1 + 100 = 4 + 97 = 101 = …..
Do đó số bị chia là: 101 x 34 : 2 = 1717
Ta có: 1717 : a = 17
a = 1717 : 17
a = 101
vậy a = 101.
b.
x - 1 2 × 5 3 = 7 4 - 1 2 x - 1 2 × 5 3 = 5 4 x - 1 2 = 5 4 : 5 3 x - 1 2 = 3 4 x = 3 4 + 1 2 x = 5 4
c. 2000 2001 v à 2001 2002
Ta có: 1 - 2000 2001 = 1 2001
1 - 2001 2002 = 1 2002
Vì 1 2001 > 1 2002 nên 2000 2001 < 2001 2002

Bài 1 :
a) \(\dfrac{12}{15}< \dfrac{12}{14}< \dfrac{13}{14}\Rightarrow\dfrac{12}{15}< \dfrac{13}{14}\)
b) \(\dfrac{11}{12}< \dfrac{11+1984}{12+1984}=\dfrac{1995}{1996}\)
\(\Rightarrow\dfrac{11}{12}< \dfrac{1995}{1996}\)
c) \(\dfrac{499}{498}>\dfrac{499+1}{498+1}=\dfrac{500}{499}\)
\(\Rightarrow\dfrac{499}{498}>\dfrac{500}{499}\)
d) \(\dfrac{51}{80}< \dfrac{51}{79}< \dfrac{53}{79}\)
\(\Rightarrow\dfrac{51}{80}< \dfrac{53}{79}\)
Bài 2:
a) \(\dfrac{1}{9\times10}+\dfrac{1}{10\times11}+\dfrac{1}{11\times12}+...+\dfrac{1}{29\times30}\)
\(=\dfrac{1}{9}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{11}+...+\dfrac{1}{29}-\dfrac{1}{30}\)
\(=\dfrac{1}{9}-\dfrac{1}{30}\)
\(=\dfrac{10}{90}-\dfrac{3}{90}\)
\(=\dfrac{7}{90}\)
b) \(\dfrac{2}{7\times9}+\dfrac{2}{9\times11}+\dfrac{2}{11\times13}+....+\dfrac{2}{37\times39}\)
\(=\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+...+\dfrac{1}{37}-\dfrac{1}{39}\)
\(=\dfrac{1}{7}-\dfrac{1}{39}\)
\(=\dfrac{32}{273}\)
c) \(\dfrac{1}{1\times4}+\dfrac{1}{4\times7}+...+\dfrac{1}{31\times34}\)
\(=\dfrac{1}{3}\cdot\left[3\cdot\left(\dfrac{1}{1\times4}+\dfrac{1}{4\times7}+...+\dfrac{1}{31\times34}\right)\right]\)
\(=\dfrac{1}{3}\cdot\left(\dfrac{3}{1\times4}+\dfrac{3}{4\times7}+...+\dfrac{3}{31\times34}\right)\)
\(=\dfrac{1}{3}\cdot\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{31}-\dfrac{1}{34}\right)\)
\(=\dfrac{1}{3}\cdot\left(1-\dfrac{1}{34}\right)\)
\(=\dfrac{1}{3}\cdot\dfrac{33}{34}\)
\(=\dfrac{11}{34}\)

a. A= 101 x 50
B = 50 x 49 + 53 x 50
= 50 x (49 + 53)
= 50 x 102
Vì 50 = 50 và 101 < 102 Nên A < B.
b. Đảo ngược mỗi phân số đã cho
Viết 13 27 đảo ngược thành 27 13
Viết 7 15 đảo ngược thành 15 7
So sánh 27 13 và 15 7
Ta có: 27 13 = 2 1 13 và 15 7 = 2 1 7
Vì 1 13 < 1 7 nên 2 1 13 < 2 1 7
Do đó 27 13 < 15 7
Vì 27 13 < 15 7 nên 13 27 > 7 15

1.
a) \(\frac{6}{15}+\frac{6}{35}+\frac{6}{63}+\frac{6}{99}+\frac{6}{143}\)
\(=\frac{6}{3.5}+\frac{6}{5.7}+\frac{6}{7.9}+\frac{6}{9.11}+\frac{6}{11.13}\)
\(=\frac{6}{2}\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+...+\frac{1}{11}-\frac{1}{13}\right)\)
\(=\frac{6}{2}\left(\frac{1}{3}-\frac{1}{13}\right)\)
\(=\frac{6}{2}.\frac{10}{39}\)
\(=\frac{10}{13}\)
b) \(\frac{3}{24}+\frac{3}{48}+\frac{3}{80}+\frac{3}{120}+\frac{3}{168}\)
\(=\frac{3}{4.6}+\frac{3}{6.8}+\frac{3}{8.10}+\frac{3}{10.12}+\frac{3}{12.14}\)
\(=\frac{3}{2}\left(\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+\frac{1}{8}-\frac{1}{10}+...+\frac{1}{12}-\frac{1}{14}\right)\)
\(=\frac{3}{2}.\left(\frac{1}{4}-\frac{1}{14}\right)\)
\(=\frac{3}{2}.\frac{5}{28}\)
\(=\frac{15}{56}\)
\(a.\frac{6}{3.5}+\frac{6}{5.7}+...+\frac{6}{11.13}\)
\(=3.\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{11}-\frac{1}{13}\right)\)
\(=3.\left(\frac{1}{3}-\frac{1}{13}\right)\)
\(=3.\frac{10}{39}\)
\(=\frac{10}{13}\)
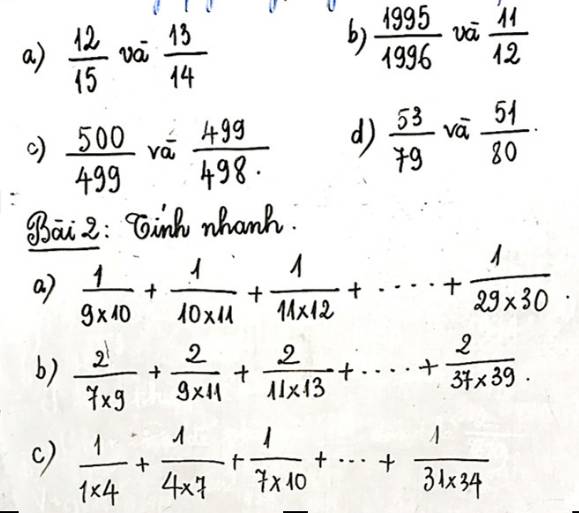
Bài 1
\(\left(1-\dfrac{1}{99}\right)\times\left(1-\dfrac{1}{100}\right)\times...\times\left(1-\dfrac{1}{2006}\right)\)
\(=\dfrac{98}{99}\times\dfrac{99}{100}\times...\times\dfrac{2005}{2006}\)
\(=\dfrac{98}{2006}\)
\(=\dfrac{49}{1003}\)
Bài 2
\(\dfrac{111}{333}=\dfrac{111:111}{333:111}=\dfrac{1}{3}\)
\(\dfrac{2222}{4444}=\dfrac{2222:2222}{4444:2222}=\dfrac{1}{2}\)
Do \(3>2\Rightarrow\dfrac{1}{3}< \dfrac{1}{2}\)
Vậy \(\dfrac{111}{333}< \dfrac{2222}{4444}\)
Bài 1.
\(\left(1-\dfrac{1}{99}\right)\times\left(1-\dfrac{1}{100}\right)\times...\times\left(1-\dfrac{1}{2006}\right)\)
\(=\dfrac{98}{99}\times\dfrac{99}{100}\times...\times\dfrac{2005}{2006}\)
\(=\dfrac{98\times99\times...\times2005}{99\times100\times...2006}\)
\(=\dfrac{98}{2006}\)
\(=\dfrac{49}{1003}\)
Bài 2.
Có: \(\dfrac{111}{333}=\dfrac{111}{3\times111}=\dfrac{1}{3}\)
\(\dfrac{2222}{4444}=\dfrac{2222}{2\times2222}=\dfrac{1}{2}\)
Vì \(\dfrac{1}{3}< \dfrac{1}{2}\) nên \(\dfrac{111}{333}< \dfrac{2222}{4444}\)