Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình chuyển động của ô tô : x A = 80t
Phương trình chuyển động của xe máy : x B = 20 + 40t

Hai xe gặp nhau khi x A = x B . Từ đó suy ra :
- Thời điểm hai xe gặp nhau kể từ khi xuất phát : 80t = 20 + 40t
Hay t = 20/40 = 0.5(h)
- Vị trí hai xe gặp nhau cách A một đoạn : x A = 80.0,5 = 40 km.

a/ Phường trình CĐ : \(x=50t\left(km\right)\)
b/ Lúc 7 giờ xe cách gốc tọa độ A là : \(x=50.1=50\left(km\right)\)
c/ \(t=\dfrac{x}{v}=\dfrac{100}{50}=2\left(h\right)\)
Khi đó xe đến B lúc 8h

Đồ thị toạ độ của hai xe có dạng như trên hình I.1G, trong đó đường I biểu diễn chuyển động của ô tô và đường II biểu diễn chuyển động của xe máy.
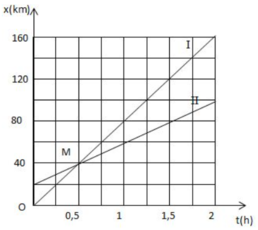
Căn cứ vào đồ thị trên hình I.l G, ta thấy hai đường biểu diễn I và II giao nhau tại điểm M ứng với thời điểm hai xe gặp nhau t = 0,5 giờ = 30 phút ở vị trí có toạ độ x = 40 km.
Như vậy kết quả tìm được trên đồ thị trùng với kết quả tính toán trong câu b).
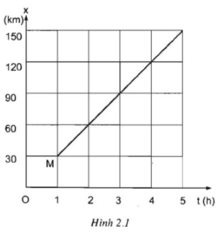
a, \(x_1=30t\left(km,h\right)\)
b,\(x_2=-60+30\left(t+1\right)\left(km,h\right)\)
c,\(x_3=-40+30\left(t-1\right)\left(km,h\right)\)
d,\(x_4=20-30\left(t-0,5\right)\left(km,h\right)\)
e, Khi người đi xe đạp đến B
\(0=-60+30\left(t+1\right)\Rightarrow t=1\left(h\right)\)
vậy thời điểm ng đi xe đạp đến B là 6 +1=7(h)