Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

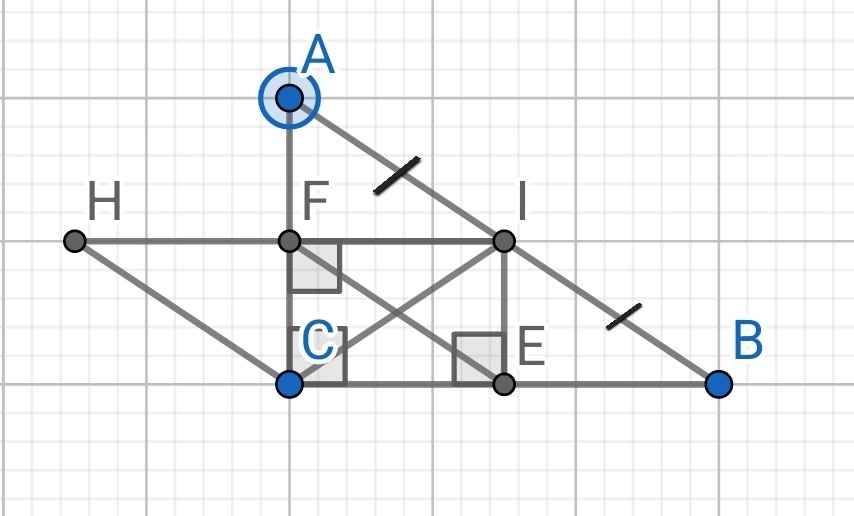 *) Tứ giác CEIF là hình gì?
*) Tứ giác CEIF là hình gì?
Tứ giác CEIF có:
∠CEI = ∠CFI = ∠ECF = 90⁰ (gt)
⇒ CEIF là hình chữ nhật
*) Do CEIF là hình chữ nhật (cmt)
⇒ FI = CE và FI // CE
Do FI // CE (cmt)
⇒ FH // CE
Do FI = CE (cmt)
FI = FH (gt)
⇒ FH = CE
Tứ giác CHFE có:
FH // CE (cmt)
FH = CE (cmt)
⇒ CHFE là hình bình hành
Sửa đề: IF vuông góc AC tại F
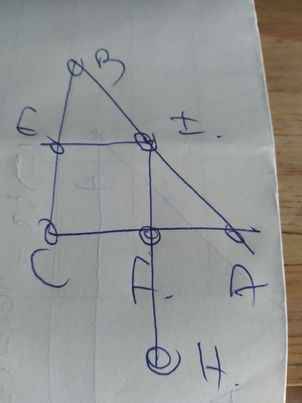
a: Xét tứ giác CEIF có
\(\widehat{CEI}=\widehat{CFI}=\widehat{FCE}=90^0\)
Do đó: CEIF là hình chữ nhật
b: CEIF là hình chữ nhật
=>CE//FI và CE=FI
CE=FI
FI=FH
Do đó: CE=FH
CE//FI
\(F\in IH\)
Do đó: CE=FH
Xét tứ giác CEFH có
CE//FH
CE=FH
Do đó: CEFH là hình bình hành

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

Vì câu a sai đề nên giải câu b nhé
b, ΔABCΔABC có: AD là trung tuyến ⇒AD=BD=DC=12BC⇒AD=BD=DC=12BC(trung tuyến thuộc cạnh huyền) ⇒ΔABD⇒ΔABD cân tại D có DF là đường cao ⇒⇒DF là trung tuyến
Tứ giác ADBG có 2 đường chéo AB và DG cắt nhau tại trung điểm mỗi đường ⇒⇒Tứ giác ADBG là hình bình hành có AD=BD(cmt)⇒AD=BD(cmt)⇒Hình bình hành ADBG là hình thoi
# Chúc bạn học tốt!

Đánh dấu mỗi bao từ 1 đến 12, tương ứng đó cứ mỗi bão ta lấy 1 đồng xu theo cách bao 1 lấy 1 đồng, bao 2 lấy 2 đồng, bao 3 lấy 3 đồng, dùng cách đó với các bao còn lại. Với mỗi đồng xu bằng 10 gram tương đương đó ta sẽ có phép tính đơn giản là 10 x (1+2+3+4+5+6+7+8+9+10+11+12) = 780 gram. Lấy ví dụ bao 8 tương đương với 8 đồng xu là bao có đồng xu giảm tương đương với 10 - 1 = 9 ta sẽ được phép tính 10 x (1+2+3+4+5+6+7+9+10+11+12) + 9 x 8 = 772 gram. Ta thấy con số theo đúng với mỗi bao 10 gram là 780 gram nhưng ở đây khi thay một bao trong số đó là bao giả ta sẽ có con số khác 780 gram và lấy ví dụ trên là 772, 780 - 772 = 8 tương ứng với bao số 8. Giả sử cũng như vậy nhưng lấy bao số 6 là đồng xu giả ra ta sẽ có 774 gram và 780 - 774 = 6. Nguyên lí là 10 x a = 9 x a + 1 x a, ở đây với bao giả ta phải bỏ đi 1 x a đó. Với cách thức như trên thì chỉ cần 1 lần đo là tìm ra bao giả như đề bài yêu cầu.

Bài 1:
a) Xét tam giác ABC có M là trung điểm của AB (gt) ,E là trung điểm của AC (gt)
\(\Rightarrow ME\)là đường trung bình tam giác ABC
\(\Rightarrow ME=\frac{1}{2}BC\left(tc\right)\left(1\right)\)
Xét tam giác ADC có E là trung điểm của AC (gt) ,P là trung điểm của DC (gt)
\(\Rightarrow PE\)là đường trung bình của tam giác ADC
\(\Rightarrow PE=\frac{1}{2}AD\left(tc\right)\left(2\right)\)
mà \(AD=BC\left(gt\right)\left(3\right)\)
Từ (1) , (2) và (3) \(\Rightarrow EM=PE\)
CMTT: \(PE=FP,FM=ME\)
\(\Rightarrow ME=EP=PF=FM\)
Xét tứ giác MEPF có:
\(ME=EP=PF=FM\left(cmt\right)\)
\(\Rightarrow MEPF\)là hình thoi ( dhnb)
b) Vì \(MEPF\)là hình thoi (cmt)
\(\Rightarrow FE\)giao với MP tại trung điểm mỗi đường (tc) (4)
Xét tam giác ADB có M là trung điểm của AB(gt) ,Q là trung điểm của AD (gt)
\(\Rightarrow MQ\)là đường trung bình của tam giác ADB
\(\Rightarrow MQ//DB,MQ=\frac{1}{2}DB\left(tc\right)\left(5\right)\)
Xét tam giác BDC có N là trung điểm của BC(gt) , P là trung điểm của DC(gt)
\(\Rightarrow NP\)là đường trung bình của tam giác BDC
\(\Rightarrow NP//DB,NP=\frac{1}{2}DB\left(tc\right)\left(6\right)\)
Từ (5) và (6) \(\Rightarrow MQ//PN,MQ=PN\)
Xét tứ giác MQPN có \(\Rightarrow MQ//PN,MQ=PN\)
\(\Rightarrow MQPN\)là hình bình hành (dhnb)
\(\Rightarrow MP\)giao QN tại trung điểm mỗi đường (tc) (7)
Từ (4) và (7) \(\Rightarrow MP,NQ,EF\)cắt nhau tại một điểm
c) Xét tam giác ABD có Q là trung điểm của AD (gt), F là trung điểm của BD(gt)
\(\Rightarrow QF\)là đường trung bình của tam giác ADB
\(\Rightarrow QF//AB\left(8\right)\)
CMTT: \(FN//CD\)và \(EN//AB\)
Mà Q,F,E,N thẳng hàng
\(\Rightarrow AB//CD\)
Vậy để Q,F,E,N thẳng hàng thì tứ giác ABCD phải thêm điều kiện \(AB//CD\)
Bài 2:
a: Xét tứ giác CEIF có \(\widehat{CEI}=\widehat{CFI}=\widehat{FCE}=90^0\)
nên CEIF là hình chữ nhật