Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
a)Ta có góc BEH =90 độ (góc nội tiếp chắn nửa đường tròn)
và góc FHC = 90 độ (góc nội tiếp chắn nửa đường tròn)
Xét tứ giác AFHE , ta có:
góc EAF =90 độ (tam giác ABC vuông tại A)
góc AEH =90 độ (cmt)
góc AFH=90 độ (cmt)
=> tứ giác AFHE là hình chữ nhật (tứ giác có 3 góc vuông)
b)Gọi I là giao điểm của AH và EF
Ta có: AH=EF (hcn AFHE) (1)
mà 2 đường chéo AH và EF cắt nhau tại I (vẽ thêm)
=>I là trung điểm của AH và EF (2)
từ (1) và (2)=> IE=IH=IA=IF
Ta có: góc IHF =góc ACH (phụ với góc HAC)
mà góc IHF = góc IFH (tam giác IHF cân tại I (IH=IF) )
=>góc ACH = góc IFH (cùng = góc IHF)
mà góc IFH= góc AEF (2 góc so le trong của AE song song HF(cùng vuông góc AC))
=>góc AEF =góc ACH=>tứ giác BEFC nội tiếp đường tròn
c)Gọi J là tâm của nửa đường tròn đường kính BH
và K là tâm của nửa đường tròn đường kính HC
Ta có: tam giác KFC cân tại K (KF=KC)
=>góc KFC = góc KCF mà góc KCF=góc IFH (cmt)
=>góc KFC =góc IFH (cùng =góc KCF)
mà góc KFC + góc HFK =90 độ (góc HFC =90 độ)
=>góc IFH + góc HFK =90 độ => góc IFK =90 độ
=>EF là tiếp tuyến của nửa (K) (I thuộc EF) (3)
Ta lại có: tam giác JEH cân tại J (JE=JH)
=> góc JEH =góc JHE
mà góc JHE = góc HCF ( 2 góc so le trong của HE song song CA ( cùng vuông góc AB) )
và góc HCF = góc AEF (cmt)
=>góc JEH= góc AEF
mà góc AEF + góc HEF = 90 độ (góc HEA = 90 độ)
=>góc JEH + góc HEF =90 độ => góc JEF = 90 độ
=>EF là tiếp tuyến của nửa (J) (4)
Từ (3) và (4) => EF là tiếp tuyến chung 2 nửa dường tròn dường kính BH và HC

2: ΔABC vuông tại A nội tiếp (O)
=>O là trung điểm của BC
BC=căn 6^2+8^2=10cm
=>OB=OC=10/2=5cm
S=5^2*3,14=78,5cm2

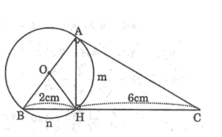
Ta có AB=4cm ⇒ OB =2cm
Tam giác OBH có OB = OH =HB = 2cm nên tam giác OBH đều

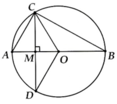
a, AC = 4cm => BC = 4 3 cm
=> R = 4cm => C = 8πcm, S = 16π c m 2
b, ∆AOC đều => A O C ^ = 60 0
=> C O D ^ = 120 0 => l C A D ⏜ = π . 4 . 120 180 = 8 π 3 cm
=> S = 8 π 3 . 4 2 = 16 π 3 c m 2

M N Q H 2 6 O
a) \(MN^2=NH.NQ=2.\left(2+6\right)=16\)
=> MN = 4 (cm). => Bán kính hình tròn tâm O là MN/2 = 2 (cm)
=> Diện tích hình tròn tâm O là: 2.2.3,14 = ...12,56 (cm2)
b) Ta có tam giác ONH là tam giác đều (vì ON = OH = HN = 2).
Suy ra \(\widehat{NOH}=60^o\) => \(\widehat{MOH}=180^o-60^o=120^o\)
=> Diện tích quạt tròn MOH là: \(\frac{12,65}{360}.120=\frac{12,65}{3}\left(cm^2\right)\)