Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC vuông tại B ta có:
\(AB^2+BC^2=AC^2\)
\(\Leftrightarrow12^2+5^2=AC^2\)
\(\Leftrightarrow AC^2=169\)
\(\Leftrightarrow AC=13cm\)
Xét tam giác ABC vuông tại H, đường cao BH:
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(AB^2=AH.AC\)
\(\Leftrightarrow12^2=AH.13\)
\(\Leftrightarrow144=AH.13\)
\(\Leftrightarrow AH=\dfrac{144}{13}cm\)
\(HC=AC-AH\)
\(\Leftrightarrow HC=13-\dfrac{144}{13}\)
\(\Leftrightarrow HC=\dfrac{25}{13}cm\)

a: Xét ΔHDC có
N là trung điểm của HD
M là trung điểm của HC
Do đó: NM là đường trung bình của ΔHDC
Suy ra: NM//DC và \(NM=\dfrac{CD}{2}\)
mà AB//DC và \(AB=\dfrac{CD}{2}\)
nên NM//AB và NM=AB
b: Xét tứ giác ABMN có
AB//NM
AB=NM
Do đó: ABMN là hình bình hành

a) Tính MN:
Xét tam giác ABC ta có:
M là trung điểm AC (gt); N là trung điểm BC (gt)
=>MN là đường trung bình của tam giác ABC
=> MN // BC; MN=BC/2
=>MN= 12/2=6
b) Tính diện tích tam giác ABC:
Xét tam giác ABC vuông tại A ta có:
AB2+AC2=BC2 (định lý Pytagor thuận)
122+AC2=202
144+AC2=400
AC2=400-144=256
AC=16
Diện tích tam giác ABC là:
S tam giác ABC= AB*AC=12*16=192
c) CMR: tứ giác ABCD là hình bình hành:
Xét tứ giác ABCD ta có:
M là trung điểm của AC (gt)
M là trung điểm của BD (gt)
AC cắt BD tại M
=> tứ giác ABCD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
d) CM: tứ giác ABEC là hình chữ nhật:
Ta có :
CD=AB ( ABCD là hình bình hành)
CD=CE (gt)
=>CE=AB
Xét tứ giác ABEC ta có:
AB=CE (cmt)
AB//CE (AB//CD; C thuộc DE)
=>tứ giác ABEC là hình bình hành ( tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau)
mà góc BAC= 900 (tam giác ABC vuông tại A)
=.>hình bình hành ABEC là hình chữ nhật (tứ giác là hình bình hành có một góc vuông)

e) Chứng minh HI, ST, KF đồng quy.
Gọi O là giao điểm của EI và HK.
Xét tứ giác HIKE ta có:
góc IHE = 900 (HI _|_ EB tại H)
góc IKE = 900 (KI _|_ EC tại K)
góc HEK = 900 (tứ giác ABEC là hình chữ nhật)
=> tứ giác HIKE là hình chữ nhật (tứ giác có 3 góc vuông)
=> góc HIK = 900
=> KI _|_ HI tại I
Xét hình chữ nhật HIKE ta có:
2 đường chéo EI và HK cắt nhau tại O (cách vẽ)
=> O là trung điểm của EI và O là trung điểm của HK
Xét tam giác FEI vuông tại F ta có:
FO là đường trung tuyến ứng với cạnh huyền EI (O là trung điểm của EI)
=> FO = 1/2 EI
Mà EI = HK (tứ giác HIKE là hình chữ nhật)
Nên FO = 1/2 Hk
Xét tam giác FHK ta có:
FO là đường trung tuyến (O là trung điểm của HK)
FO = 1/2 HK (cmt)
=> tam giác FHK vuông tại F
=> HF _|_ FK tại F
Xét tam giác SHK ta có:
ST là đường cao (ST _|_ HK tại T)
HI là đường cao (HI _|_ KI tại I)
KF là đường cao (KF _|_ HF tại F)
=> HI, ST, KF đồng quy tại một điểm (đpcm)

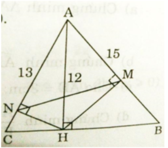
a) Xét ΔANH và ΔAHC có:
∠(NAH) chung
∠(ANH) = ∠(AHN) = 90o
⇒ ΔANH ∼ ΔAHC (g.g)
b) Ta có :
![]()
![]()
Tương tự : CH = 5 (cm)
⇒ BC = BH + CH = 9 + 5 = 14 (cm)
c) Theo chứng minh trên ta có:
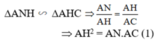
Chứng minh tương tự ta có :
ΔAMH ∼ ΔAHB ⇒ AH2 = AM.AB (2)
Từ (1) và (2) ⇒ AN.AC = AM.AB (3)
Xét ΔAMN và ΔACB có :
∠A chung
AN.AC = AM.AB
⇒ ΔAMN ∼ ΔACB (c.g.c)
d) Ta có : ΔAMH ∼ ΔAHB
![]()
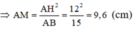
Lại có ΔAMN ∼ ΔACB (cmt)
![]()
![]()